Archiv für den Monat November 2011

Das Hühnerei

Posted on by

von Hanna Vock

 

Auch mit ganz wenigen Mitteln lässt sich naturwissenschaftliches Denken und Handeln üben.

An einem Beispiel möchte ich das demonstrieren. Im Jahr 2001 leitete ich in Düsseldorf eine Spiel- und Lerngruppe für hoch begabte Vorschulkinder. Dieses Angebot der Volkshochschule Düsseldorf fand wie geplant 10-mal statt, jedes Treffen dauerte eineinhalb Stunden, nachmittags in wöchentlichem Abstand.

Die sieben teilnehmenden Kinder waren vier Jungen und drei Mädchen im Alter von 4;8 bis 5;6 Jahren. Bis auf zwei Mädchen kannten sie sich nicht untereinander, und sie kannten mich nicht und auch nicht den Raum, in dem wir uns trafen. Alles Material musste ich mitbringen und jedes Mal wieder mit nach Hause nehmen. Trotz dieser im Vergleich zum Kindergarten ungünstigen Bedingungen stellte sich ein freudiges und intensives Spielen und Lernen ein.

…kurz gefasst…

Sieben vermutet hoch begabte Vorschulkinder befassen sich mit dem Hühnerei. Sie untersuchen es gründlich und gehen der spannenden Frage nach, warum Eier mit zunehmendem Alter anfangen, in Wasser zu schwimmen. Und sie kriegen es heraus.

Wir befassten uns an den 10 Nachmittagen mit verschiedenen Themen, eins davon war „Das Ei“. Die Kinder sollten das Hühnerei gründlich erforschen können, daran sollten sie Entdeckungen machen und sich darüber austauschen.

Wichtig war mir dabei, dass die Kinder

  • Veränderungen über die Zeit beobachten konnten,
  • eine Möglichkeit kennen lernen sollten, ihre Beobachtungen zu notieren,
  • erfahren sollten, dass gemeinsames Nachdenken über das Beobachtete, genaues Schlussfolgern helfen, eine zunächst „geheimnisvolle“ Frage zu klären,

was ja alles grundlegende naturwissenschaftliche Vorgehensweisen sind.

Siehe auch: Wie geschieht Lernen und Forschen?

Die Kinder erhielten rohe und gekochte Hühnereier, die sie auseinander nehmen und untersuchen konnten. Das alles fand unter allerhand Vorkehrungen auf dem Teppichboden des VHS-Raums statt. Die Kinder entdeckten, wie das Ei innen aussieht, wie es riecht und sich anfühlt.

Alle Beobachtungen, die die Kinder machten, trugen wir in der Gruppe zusammen. Dabei kam es auf genaue Beschreibung und präzise Formulierung an.

Interessant war, dass die Kinder sich selbst, aber sich auch gegenseitig immer wieder präzisierten.

Nach den Angaben der Kinder versuchte ich an der Tafel eine Skizze, die immer wieder verändert wurde, bis die Kinder mit der Skizze zufrieden waren. Dabei wurde auch über die Beschaffenheit und den Sinn und Zweck der Ei-Bestandteile diskutiert. Danach wurde die Skizze an der Tafel weggewischt, und die Kinder versuchten, die besprochenen Einzelheiten aus dem Gedächtnis zu zeichnen.

Anhand von Skizzen und aus mitgebrachten Fotos wurden die Einzelheiten des Eies mit der Entwicklung des Kükens im Ei zusammengebracht.

Beim Reden über die Form und den Ursprung des Eies entstand spontan das Gedicht:

Das Ei ist nicht eckig und nicht spitz.
Das wäre auch kein guter Witz.
Das ist auch nicht egal.
Es wär fürs Huhn ne schlimme Qual.
Zum Glück ist jedes Ei oval.

Die Kinder rätselten darüber, welches „Fach“ sie denn nun gehabt hätten, wenn das Ganze jetzt in der Schule stattfinden würde. (Sie waren alle noch Monate bis Jahre von der Einschulung entfernt.) Nachdem ich ihnen die üblichen Schulfächer (und was da so gemacht wird) aufgezählt hatte, fanden sie am Ende dieser Diskussion, dass es sich wohl um eine Mischung aus Naturwissenschaft und Deutsch und Kunst gehandelt haben müsste. Diese Einschätzung fand ich bemerkenswert.

Um noch mehr über das Hühnerei herauszufinden, schlug ich den Kindern den Eier-Frische-Test vor. (Das Ei ist frisch, wenn es in einer Schale mit Wasser unten auf dem Boden liegen bleibt.)

Nachdem die Kinder festgestellt hatten, dass manche Eier auf dem Boden liegen blieben, manche sich im Wasser aufstellten und manche sogar schwammen, drehte sich alles um die Frage:

Warum ist das so unterschiedlich?

Die Kinder erhielten einige wichtige Informationen: Anhand ihrer Zeichnungen des Ei-Aufbaus erfuhren sie,

  • dass die Kalkschale kleine Löcher hat, durch die Wasser raus und Luft rein gelangen kann;
  • dass das Eiweiß und das Eigelb sich so nass anfühlen, weil da auch Wasser drin enthalten ist;

Außerdem:

  • dass Wasser verdunsten (in die Luft gehen) kann und die vorher nassen Sachen dadurch trockener werden (zum Beispiel aufgehängte Wäsche);
  • dass manche Dinge schwimmen können, wenn man sie mit Luft aufbläst (zum Beispiel Schwimmflügel).

Sie konnten diese Informationen noch nicht auf Anhieb gedanklich so weit verarbeiten, dass sie auf die Lösung kamen, warum manche Eier schwimmen und manche nicht.

Dieser Eier-Frische-Test sollte uns daher über Wochen beschäftigen, was ursprünglich gar nicht geplant war. Jede Woche wiederholten wir den Frische-Test, immer mit denselben (gekennzeichneten und anfangs frischen) Eiern und beobachteten, wie sich die Lage des Eies im Wasser von Woche zu Woche veränderte. Die Eier hielten den vielfachen Hin- und Her- Transport und auch das Hantieren der Kinder bis zum Schluss aus, ohne zu zerbrechen.

Da einige Kinder große Lust hatten, an der Tafel zu schreiben, betrachteten wir das Ei auch von dieser Seite:

Die Kinder malten Ovale an die Tafel und alle anderen geometrischen Formen, die ihnen einfielen. Sie überlegten, in welchen Wörtern „ei“ vorkommt und schrieben sie (mit mehr oder weniger Anleitung) an die Tafel, zum Teil auch auf Papier.

Dabei gewann ich auch nebenbei Informationen über die Lesekompetenz der Kinder: Von den sieben Kindern lasen zwei Kinder fließend, zwei Kinder buchstabierten langsam, die anderen kannten mehr oder weniger Buchstaben.

Ergebnis, verkleinert (Junge, 5 Jahre)

Der Austausch von Wissen über die Lebensbedingungen der Hühner sowie eine Diskussion darüber rundeten das Thema vorerst ab.

Immer noch aber hatten wir das Geheimnis, warum manche Eier nicht schwimmen und manche es doch tun, noch nicht gelüftet.

 

 

 

 

 

Beim 5. Treffen, vor der Herbstferien-Pause, wiederholten wir den Eier-Frische-Test noch ein weiteres Mal. Die anfänglich noch recht frischen Eier waren natürlich gealtert. Die Kinder hatten über die Wochen beobachtet, wie sich die Lage der Eier im Wasser verändert hatte und konnten das gut beschreiben.

Sie erhielten ein vorbereitetes Blatt, auf dem die ersten drei Zustände bereits von mir eingezeichnet waren.

Sie sollten nun ihre Vermutung darüber einzeichnen, wie die Eier nach den Ferien im Wasser liegen würden. Nach den Ferien wollten wir dann die Probe machen und die tatsächliche Lage einzeichnen.

Diese Aufgabe forderte die Fähigkeit der Kinder heraus, Vermutungen über eine zukünftige Entwicklung anzustellen. Gleichzeitig lernten sie, dass Versuchsbeobachtungen mit einfachen Skizzen aufgezeichnet werden können.

Ergebnis (Junge, 5 Jahre)

 

 

 

 

Ergebnis (Mädchen, 5 Jahre)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Nach den Ferien stellte sich heraus, dass die Kinder im Prinzip richtig vermutet hatten:

Die Eier hatten sich ganz vom Boden gelöst.

Mehrere Kinder bemerkten jetzt aber, dass die Eier nicht im Wasser schwebten, sondern richtig schwammen, also teilweise aus dem Wasser auftauchten. Sie zeichneten das genau ein.

Nun erschien es mir an der Zeit, den Kindern zu helfen, die Ursache für die neu erworbene Schwimmkunst der Eier endgültig herauszufinden.

Die Frage lautete: Warum schwimmen die Eier jetzt?

Zunächst sahen wir uns noch mal unsere Zeichnungen vom Ei-Inneren an.
Über die Frage: welcher Teil des Eies könnte für das Schwimmen wichtig sein? kamen die Kinder auf die Luftkammer, da sie sich an den früher angestellten Vergleich mit den Schwimmflügeln erinnerten.

Der nächste Schritt war die Frage: Aber am Anfang, als die Eier noch frisch waren, hatten sie auch schon eine Luftkammer und konnten trotzdem nicht schwimmen. Was ist mit den Eiern passiert, dass sie es nun doch können?

Über den humorvollen Einwurf eines fünfjährigen Mädchens: „Vielleicht hat sie ja wer aufgepustet?“ kamen die Kinder nach angestrengtem Nachdenken auf die Idee, dass die Luftkammer vielleicht wirklich größer geworden ist und der Rest vom Ei dafür kleiner.

Die nächste hilfreiche Frage lautete: Kann denn in das Ei etwas rein und etwas raus gelangen, auch wenn die Schale heile ist? Hier erinnerten sich die Kinder an die feinen Löcher der Eierschale und meinten Ja.

Die abschließende Frage: Was ist denn rein und was ist raus gekommen?

Hierzu meinten die Kinder, dass wohl Luft rein gekommen und die Luftblase dadurch größer geworden ist. Raus gekommen sein müsste auch was, aber was?

Dazu war noch eine kurze Analogie nötig: Was passiert beim Wäsche trocknen auf einer Leine? Antwort: Das Wasser geht raus. Frage: wohin geht es? Antwort: irgendwie in die Luft. Frage: kann das beim Ei auch passiert sein? Ist denn im Ei überhaupt Wasser drin? Antwort: „Ja, ich glaube; es fühlt sich ja ganz nass an, … vor allem das Eiweiß.“

Die Kinder hatten ihre kleinen grauen Zellen benutzt, um einen rätselhaften Fall zu lösen, und waren sichtlich zufrieden, dass sie es geschafft hatten.

Datum der Veröffentlichung: Mai 2011
Copyright  © Hanna Vock 2011, siehe Impressum.

Kleine Experimente mit Schnee

Posted on by

von Isabel Bonifert-Manig

 

Eines Nachmittags – es waren in meiner Gruppe noch 8 Kinder da – stellte ich eine Schüssel mit Schnee in den Gruppenraum und wartete, was passieren würde. Es war also kein Versuchsaufbau vorbereitet, sondern wir tasteten uns von Versuch zu Versuch.

Jedes Kind arbeitete an einem Einzeltisch und durfte so lange versuchen, wie es wollte und bis es „satt“ war. Sobald ein Kind etwas herausgefunden hatte, schauten alle zu und das Kind erklärte, was es erforscht hat. Ich ließ die Kinder ausprobieren und stellte ihnen – entsprechend ihren Ideen – das nötige Material zur Verfügung, soweit sie es sich nicht selber zusammensuchen konnten. Am Ende setzten wir uns an einen Tisch, und die Kinder diktierten mir, was ich aufschreiben sollte. Jedes Kind hat den Ablauf und seine Schlussfolgerungen nach dem Experiment selber formuliert, so wie es hier notiert ist.

Die Kinder hatten schon Erfahrung mit dem Experimentieren, einige sind besonders begabt.

Aus Gründen der Anonymität wurden die Namen geändert.

1. Michael (4;11 Jahre):

„Schnee wird in einem Töpfchen über die Kerze gehalten.
Schnee schmilzt und wird Wasser. Ich fülle es in ein Glas und gebe es meiner Mama.“

2. Justin (5;0 Jahre):

„Schnee und Salz schmilzt auch, aber langsam. Es entstehen erst so Löcher, dann wird´s wässrig. Es geht auch alles irgendwie an die Wand. Es schmeckt ganz salzig.“

3. Rebecca (4;9 Jahre):

„Blau gefärbtes Wasser und Schnee zusammentun. Es schmilzt. Am Ende habe ich nur blaues, kaltes Wasser.“

4. Marie (5;9 Jahre)

findet heraus, dass „der blaue Schnee erst zu Eis wird – und dann erst Wasser.“

5. Adam (4;9 Jahre):

„Ich schütte kochendes Wasser in den Schnee. Ganz schnell wird alles zu Wasser. Man muss vorsichtig sein mit dem heißen Wasser.“

6. Michael (4;11 Jahre):

„Schnee anzünden. Er wird braun. Die Flamme geht nicht aus, aber es gibt zischende braune Flecken.“

7. Justin und Rebecca:

„Schnee schmilzt auf der Zunge, wird zu Wasser und man kann es trinken.“

(Achtung, Achtung: Mit Eis aus Wasser darf man dies nicht machen. Sehr kaltes Eis klebt an der Zunge fest.)

8. Justin:

„Kerzenwachs in Schnee tropfen. Es gibt einen Klumpen, keine Platte.“

Erstaunlich war, wie knapp und präzise die Kinder formulierten und wie diszipliniert und aufmerksam sie die ganze Zeit über waren. Voraussetzung dafür ist sicher, dass die Kinder viel Zeit, Raum und ungestörte Arbeitsruhe bekommen, um zu probieren und zu reflektieren: Was ist da eigentlich passiert?

Sie haben durch die kleinen Experimente durchaus Neues erfahren und konnten dabei ihre Fähigkeiten zum genauen Beobachten und Formulieren einsetzen. Sie zeigten aber auch eine bereits gut entwickelte Fähigkeit, dicht und genau am Phänomen zu bleiben – für wissenschaftliches Forschen eine wichtige Voraussetzung.

Datum der Veröffentlichung: 10.11.09

©Copyright Hanna Vock 2009, siehe Impressum

Projekte zu physikalischen und/oder chemischen Erkundungen

Posted on by

 

Spielerische Mathematik im Kindergarten

Posted on by

 von Klaudia Kruszynski

 

Zu den beliebtesten Kinderspielen gehören Spiele, die mit Sortieren, Ordnen, Zählen zu tun haben.

Diese Vorliebe lässt sich mit der Entwicklung des Intellekts erklären. Zu beobachten ist sie bei allen Kindern im Kindergarten, obwohl sie bei verschiedenen Kindern unterschiedlich stark ausgeprägt und fortgeschritten ist.

Dazu benutzen Kinder verschiedene Gegenstände.

Als Beispiel kann ich nennen: das Sortieren der Magnetbuchstaben nach Farben oder Ordnen in zwei Gruppen: Buchstaben und Ziffern. Etwas Ähnliches passiert bei den Steckspielen oder Perlenketten.

Wenn die Kinder keine Lust haben zu malen, sortieren sie die Stifte nach Farben, Länge oder danach, ob sie angespitzt werden müssen oder nicht.

Im Stuhlkreis erkennen die Kinder, ob alle da sind, ohne zu zählen, ohne zu wissen, wie viele da sind. Sie erkennen es daran, dass alle Stühle besetzt sind. (Jedem Stuhl ist ein Kind zugeordnet.) Eine andere Relation ist: Im Waschraum sind viele Zahnputzbecher – jedes Kind hat einen eigenen. Aber es ist nur eine Tube Zahncreme da – die gehört allen Kindern.

Viele Gesellschaftsspiele nutzen diese Vorliebe. Sie sind so konzipiert, dass der gewürfelten Farbe ein Plättchen/Stecker/Püppchen/Feld zugeordnet wird. Diese Spiele werden von den Jüngsten gespielt, bis sie sie als zu einfach erkennen und nicht mehr spielen wollen, oder sie überlegen sich eigene Varianten. So werden die Spielfiguren nicht mehr gesetzt, sondern zu einer Pyramide gestapelt. Dies ist schwieriger als nach der Farbe vorwärts zu gehen. In manchen Kindergärten sieht man diese Zweckentfremdung nicht so gerne, weil man überzeugt ist: Gesellschaftsspiele sind gut zum Erlernen von Regeln. Wer sich an die Regeln nicht hält, der kann sich später in der Gesellschaft nicht zu Recht finden.

Meiner Überzeugung nach, brauchen die Menschen natürlich eine geregelte Welt, aber eine gewisse Unabhängigkeit und Flexibilität sind sehr wünschenswert. Sie sind nämlich die nötige Voraussetzung für Weiterentwicklung und Fortschritt. Eine gewisse Unabhängigkeit von Regeln, Ordnungsstrukturen, Vorgehensweisen usw. deutet auf Kreativität.

Sortieren

Wie ich schon am Anfang erwähnt habe, haben viele Kinder eine Vorliebe, sogar einen Drang, die Gegenstände um sich herum zu ordnen. Dafür ist es notwendig, eine Eigenschaft (später mehrere Eigenschaften) des Objektes wahrzunehmen, und sie bei den anderen Objekten wieder zu erkennen.

Beispiele mir Magnetbuchstaben:

  • Alle gleichfarbigen Buchstaben zusammenlegen,
  • Buchstaben und Zahlen voneinander trennen,
  • alle gleichen Buchstaben, unabhängig von ihrer Farbe zusammenlegen,
  • alle Buchstaben, die in meinem Namen sind, heraussuchen,
  • aus der Menge den gewünschten Buchstaben aussuchen,
  • die Buchstaben nach dem Alphabet ordnen (Alphabet nach einer Vorlage, z.B. aus einem Buch, oder aus dem Gedächtnis, zum Beispiel nach einem Lied: “A, B, C, D, E, F, G…“.),
  • die Buchstaben zusammenzählen,
  • vergleichen der Menge der gleichen Buchstaben: es gibt 5-mal „A“, aber nur 2-mal „X“,
  • das kleine „x“ als „Malzeichen“ erkennen, die anderen Operationszeichen suchen,
  • die Zahlen aufwachsend ordnen,
  • einfache Operationen legen, zum Beispiel 2 + 2 = 4,
  • Muster legen

 

 

Spiegelbilder, Symmetrie

Manche Objekte haben eine besondere Eigenschaft: Sie bestehen aus zwei gleichen Teilen, wie z. B. die Flügel eines Schmetterlings, die aber spiegelverkehrt nebeneinander liegen. Manche Objekte lassen sich mit einer gedachten Linie in zwei Hälften teilen, die auch spiegelverkehrt sind, z.B. ein Zylinderhut.

Diese Eigenschaft besitzen auch manche Buchstaben:

– A, B, C, D, E, H, I, K, M, O, T, U, V, W, X, Y.

Mit Hilfe eines Spiegels können Kinder es wunderbar erforschen.

Siehe auch: Spiegeln mit dem Spiegelbuch in Kap. 7 des Handbuchs.

Ich habe dazu ein Spiel entwickelt:

Auf den kleinen Karten sind die oben genannten Buchstaben einzeln abgebildet. Dazu gibt es die gleiche Menge Karten, auf denen nur Hälften von Buchstaben drauf sind. Auf diesen Karten ist auch die so genannte „Spiegellinie“ aufgemalt. Darauf wird der Spiegel aufgestellt, und mit seiner Hilfe kann man den ganzen Buchstaben sehen. Es gibt verschiedene Möglichkeiten, mit den Karten zu spielen:

  • die Buchstaben erkennen und benennen,
  • die Buchstabenhälften erkennen und benennen,
  • mit Hilfe des Spiegels die „Hälfte“ dem richtigen Buchstaben zuordnen,
  • ohne den Spiegel die „Hälfte“ dem richtigen Buchstaben zuordnen.

Auch geometrische Figuren lassen sich in gleiche Hälften teilen.

Manche nur mit einer Spiegellinie – ein gleichschenkliges Dreieck,

manche mit zwei Spiegellinien – ein Rechteck,

manche mit drei Linien – ein gleichwinkliges Dreieck,

manche mit unendlich vielen – ein Kreis.

Dies herauszufinden könnte zu einem interessanten Entdeckungsspiel werden.

Der Kreis ist eine besondere Form, er wird sehr gerne von den Kindern gemalt, weil man ihn braucht, um ein Gesicht oder die Sonne zu malen. Der Kreis ist, nach dem Kreuz, die nächste Form, die in der darstellerischen Entwicklung der Kinder vorkommt. Am Anfang ähnelt er einer Spirale, dann gelingt es den Kindern ihn zu schließen. Er nimmt verschiedene Gestalten an: Oval, Ei, Ellipse, bis er endlich die perfekte Form bekommt. Bei allen ihren Versuchen, den Kreis vollkommen zu malen, merken Kinder, dass es keine einfache Aufgabe ist. Manche Kinder bitten Erwachsene um Hilfe: „Kannst du mir den Kreis malen?“ – weil sie festgestellt haben, dass ihre Ergebnisse von ihrer inneren Vorstellung, wie ein richtiger Kreis auszusehen hätte, sehr entfernt sind. Andere Kinder suchen sich Hilfsgegenstände, die sie ummalen. (Hierfür ist die Fähigkeit, den Kreis zu erkennen, eine nötige Voraussetzung.)

So passiert es bei uns oft, dass die Kinder sich einen Teller aus dem Schrank holen, wenn sie ein Mandala malen wollen. Auch die Räder für selbst gebastelte Autos müssen richtige Kreise sein – dafür nehmen Kinder z.B. den Kreis von den logischen Blöcken.

Zum Kreis ist mir ein Spiel eingefallen:

Den Kreis knicken, die Teile zählen

Am Tisch sitzen Kinder in verschiedenem Alter, manche können schon Zahlen schreiben, manche noch nicht.

Am Anfang malt jeder Mitspieler mit Hilfe des Tellers einen Kreis, dann schneidet er ihn aus. Auf einem anderen Blatt ist eine einfache Tabelle. Sie hat zwei Spalten: eine für die Zahl der Knicke und eine für die gezählten Teile.

Dann wird der Kreis einmal zusammengefaltet und wieder aufgemacht – die Kinder zählen die Knicke(1) und schreiben die Zahl in die entsprechende Spalte der Tabelle. Danach werden die entstandenen Teile gezählt(2) und die Zahl ebenfalls in die richtige Spalte eingetragen.

Die jüngeren Kinder malen Striche statt Zahlen.

In dieser Weise wird das Spiel fortgeführt: 2 Knicke – 4 Teile, 3 Knicke – 6 Teile usw.

Nach dem fünften Knick fragte ich Kinder, ob sie ohne die Teile zu zählen, schon das Ergebnis wüssten.

Jan, (4 Jahre 7 Monate) wusste sofort die richtige Zahl, er zählte die Teile nur zur Kontrolle, danach füllte er die Tabelle aus, ohne den Kreis weiter zu knicken. Er sagte mir: die Knicke gehen immer um „einen“ weiter, aber die Teile machen einen Sprung über die nächste Zahl.

Simon hat dieses Phänomen auch graphisch dargestellt.

Auch Lukas (5 Jahre 1 Monat) hatte keine Probleme mit dieser Aufgabe, obwohl er es nicht so zutreffend erklären konnte.

Linea (4 Jahre 8 Monate) wollte auf Nummer sicher gehen und wagte keine Prognosen.

Das jüngste Kind (4 Jahre 1 Monat), hatte natürlich genug Mühe mit dem Zählen der entstandenen Teile und dem Malen der Striche in entsprechender Zahl. Trotzdem konnte das Kind die Aufgabe richtig und zu seiner eigenen vollen Zufriedenheit lösen.

Bei dieser Aufgabe handelt sich auch um die Verdoppelung der Zahl, aber den am Spiel beteiligten Kindern fehlt noch diese Erfahrung.

Um solche Erfahrungen zu sammeln, dafür eignet sich wunderbar unserer Spiegel.

Mit dem Spiegel kann man alles verdoppeln: die Formen und die Mengen. Dazu gäbe es viele Möglichkeiten es zu erforschen.

Andere Spiegelspiele

1. Auf kleinen Karten sind die Hälften von verschiedenen Gegenständen aufgemalt. Kinder betrachten diese mit Hilfe des Spiegels, erfahren das „Wunder“ der Vervollständigung.

2. Die gleichen Karten werden ohne den Spiegel betrachtet. Kinder erraten, von welchem Gegenstand sie die Hälfte darstellen.

3. Gesichter, die aus zwei unterschiedlichen Hälften bestehen, ergeben beim Betrachten mal ein Männergesicht, mal ein Frauengesicht.

4. Kinder malen das Spiegelbild auf (mit und auch ohne die Hilfe des Spiegels).

 

5. Kinder entwerfen eigene Karten. (Dazu müssen sie das Wissen über Spiegelungen mit eigener Kreativität verknüpfen).

 

 

 

 

 

 

 

 

 

6. Kinder betrachten verschiedene Gegenstände mit dem Spiegel, stellen fest, dass sie unterschiedliche Bilder bekommen, wenn sie die Lage des Spiegels nur ein wenig verändern.

 

 

 

 

 

 

 

 

7. Nachdem sie das Phänomen begriffen haben, legen sie „Spiegelmuster“, z. B. beim „Hammer-Spiel“.

Siehe auch: Spiegeln mit dem Spiegelbuch , unter „Interessante Spiele“ in Kap. 7 des Handbuchs.

Mengenlehre und Statistik im Kindergarten.

Im Laufe des Lebens entwickelt sich bei Kindern der Drang, die Sachen, die sie umgeben, zu sortieren. Aus dem Schrank werden Kleider in Lieblingsfarbe rausgesucht, auf eine rote Untertasse wird die rote Tasse gestellt, jede Reihe im Steckspiel wird nur in einer Farbe gelegt, die Logischen Blöcke werden nach Form eingeräumt, die Münzen werden nach der Farbe, später nach dem Wert gestapelt, usw.

Auch gezielte Spielangebote fördern diese Entwicklung, z.B. im Stuhlkreis: Kurz vor 12 Uhr holen sich die Kinder ihre Kindergartentaschen. Damit dabei kein Chaos entsteht, geben wir Hinweise, welche Kinder jetzt gehen sollen: alle, die einen roten Pullover anhaben, oder alle, die Buchstaben auf dem T-Shirt haben oder einen Zopf haben usw. Hier erlebt sich ein Kind immer zur einer bestimmten Gruppe (Menge) zugehörend, je nach dem, was es an dem Tag an hat.

Das langweilige Aufräumen kann man auch spannender gestalten, indem man extra Behälter für Spielsachen unterschiedlicher Farben, Formen oder Größen bereitstellt.

Dazu überlegte ich mir paar neue Spiele, die ich mit einer kleinen Gruppe durchgeführt habe.

Duplo-Männchen-Haus

20 Duplo-Männchen möchten in einem Haus „wohnen“. Sie sind alle unterschiedlich, deshalb wollen sie nicht in ein Zimmer. Die „Mädchen“ wollen nicht zusammen mit den „Jungen“ wohnen. Die mit roten Pullovern wollen ihr Zimmer mit denen, die blaue Pullover anhaben, nicht teilen, usw.

Dieses Spiel entwickelte sich wie eine Geschichte (andere Varianten wären natürlich möglich gewesen).


Kinder betrachteten die Püppchen und überlegten, in welches Zimmer sie sie rein legen sollen. Sie zählten die Mengen und schrieben die Zahlen auf. Manche Püppchen konnten mehreren Räumen zugeordnet werden.

Durch genaue Hinweise, die auf den „Spielkarten“ waren, konnten alle anwesenden Kinder die Aufteilung vollziehen, die älteren haben das Aufschreiben der Zahlen übernommen.

Statistische Untersuchung der Duplogesellschaft

Diesmal wollten wir uns die Duplo-Männchen genauer anschauen, jedes einzeln. Ich habe mir die wichtigsten Kriterien ausgesucht und eine statistische Tabelle vorbereitet. Diese Aufgabe forderte von den Kindern viel mehr Aufmerksamkeit, Konzentration und Ausdauer.

 

Zu meinem Erstaunen wurde dieses Spiel zu der Lieblingsbeschäftigung mehrerer Kinder, auch jüngerer.

Ich beobachtete, wie liebevoll und gleichzeitig scharfsinnig die Püppchen von den Kindern betrachtet wurden, wie die Kreuze in den entsprechenden Spalten gemacht wurden. (Manche Kinder benötigten dazu keine „Hilfsstreifen“, sie konnten die Koordinaten richtig orten.)

 

 

 

Eines Tages sprach mich Jan (4 Jahre 7 Monate,) an, er würde so gerne auch so eine Tabelle für die Kinder vorbereiten.

Ich fand das gut, und gemeinsam überlegten wir uns, dass wir diesmal Duplo-Tiere untersuchen würden.

Aus der Duplo-Tier-Kiste suchte Jan 10 Tiere aus. Wir betrachteten sie und überlegten, welche Kriterien wir nehmen könnten. Jan malte die Tabelle auf, aber er bat mich, sie mit dem Computer zu schreiben, weil es viel schöner wäre (leider steht bei uns im Kindergarten kein Computer für solche Spiele zur Verfügung – es wäre sehr spannend, Jan das Vorbereiten der Tabelle zu überlassen).

 

Auch diese Aufgabe wurde mit Begeisterung von mehreren Kindern gelöst, wobei Jan persönlich keinen besonderen Wert darauf legte, sie korrekt zu lösen, er machte sehr viele Fehler.

Zum Schluss machte Lukas eine Abschluss-Rechnung, um zu prüfen, wer die Aufgabe am genauesten gelöst hat. Dafür musste er alle Einzelergebnisse eintragen und danach mit der richtigen Zahl vergleichen. Er arbeitete sehr ausdauernd und konzentriert.

 

Potenz

Im Frühling beschäftigten wir uns mit dem Wachstum der Pflanzen. Wir beobachteten über mehrere Wochen, wie die Bohnensamen keimten, zu grünen Pflanzen heran wuchsen, Blüten bekamen. Schließlich konnten wir sehen, dass sich die Schoten mit neuen Kernen bildeten und reiften. In der ersten Septemberwoche war die Erntezeit gekommen.

Im Blumentopf waren 6 Pflanzen mit jeweils 3 Schoten.

Ich arbeitete mit einer kleinen Gruppe, die aus den Kindern bestand, die sich im Laufe der Vegetationszeit um die Bohnenpflanzen gekümmert hatten.

Jedes Kind bekam ein großes Blatt Papier, einen Stift und natürlich eine geerntete Pflanze.

Am Anfang betrachteten die Kinder die Pflanzen, wir erinnerten uns, was wir im Frühling beobachtet hatten:

Wie war das Wachstum, was haben die Pflanzen benötigt, um richtig zu wachsen usw.

Wir haben auch festgestellt, dass jede Pflanze aus einer einzelnen Bohne gewachsen ist.

Die Kinder waren schon sehr gespannt auf die Schoten, die sie schließlich öffneten. Sie staunten sehr, als sie im Inneren die weißen Kerne entdeckten.

Jedes Kind sollte seine „Bohnen-Kinder“ zählen und die Zahl aufschreiben. Die Mengen waren 14 oder 15 Kerne. Ich stellte die Frage: „Wie viele Kinder bekam die Bohnen-Mama?“ Jedes Kind gab mir die Antwort.

Danach haben wir alle „Kinder“ zusammengezählt: 88.

Ich fragte, ob sie wüssten, wie viele Kinder diese Bohnen bekommen würden, wenn wir sie im nächsten Frühling in die Erde setzten?

Das konnten sich die Kinder nicht vorstellen, sie gaben mir verschiedene Antworten.

Ich habe auf dem Blatt eine Bohne gemalt – es war die „Bohnenmama“, darunter alle 15 „Kinderbohnen“.

Zu jedem „Kind“ malte ich seine Kinder (wenn wir diese Bohne nächste Jahr in die Erde stecken würden).

Die Kinder unterstützen mich beim Malen und merkten, dass es sehr viele neue Bohnen werden.

Und wenn wir diese „Enkelbohnen“ in die Erde stecken, dann bekommen wir sehr, sehr viele Bohnen.

Bei diesem Angebot war es nicht wichtig, die wahre Natur der mathematischen Potenz exakt zu lernen. Es war wichtig, dass die Kinder ein Gefühl dafür entwickelten.

Dazu habe ich mir eine Geschichte überlegt:

Ein Gartenwichtel namens Bodo mochte sehr gerne Bohneneintopf. Deshalb setzte er im Frühling einen Bohnenkern in die Erde. Er achtete darauf, dass der Samen alles für seine Entwicklung bekam: gute Erde, Wasser, Licht und Wärme. Er betrachtete, wie seine Pflanze sich prächtig entwickelte. Auch die Nachbarn unterstützten ihn dabei.

Als der Sommer zu Ende ging, kam die Ernte. Stolz machte Bodo die 3 gelben Schoten auf und legte 15 weiße, glatte Kerne ins Körbchen. Am Sonntag wollte er Bohneneintopf kochen und dazu die netten Nachbarn einladen.

„Für einen leckeren Bohneneintopf bracht man nicht nur Bohnen“, dachte Bodo, es müssen auch noch Kartoffeln, Lauch und Karotten rein. Und dann Pfeffer und Salz. Das konnte er im Laden der schlauen Füchsin Adele bekommen. Dafür wollte Adele 5 Bohnenkerne als Bezahlung.

Und dann musste Bodo beim Biber Felix Brennholz kaufen. Felix verlangte 3 Bohnen dafür.

Als Bodo mit seinen Einkäufen nach Hause kam, stellte er fest, dass er nur 7 Bohnenkerne übrig hatte. Es war sehr wenig. Er dachte lange nach und schließlich legte er 2 Kerne in ein Holzkästchen und sagte: “Die werde ich im nächsten Frühling in die Erde stecken!“

Die letzten 5 Bohnen kochte er mit anderem Gemüse. Als die Nachbarn fragten, wieso der Bohneneintopf kaum nach Bohnen schmeckt, sagte Bodo: „Kommt nächstes Jahr zum Bohneneintopfessen!“

In dieser Geschichte ist das Wissen über die Entwicklung der Pflanzen erhalten, das die Kinder durch aktive Beobachtung gesammelt haben. Und natürlich ganz viel Mathematik. Auch einige Elemente der Wirtschaftslehre sind dabei.

Ich habe zu dieser Geschichte zusammen mit Kindern ein Bilderbuch gestaltet.

Das wurde der Abschluss unserer Bohnenzucht und gleichzeitig unserer Beitrag zum Thema: „Erntedankfest“.

Jeder Anlass im Kindergarten ermöglicht es uns Erzieherinnen, Kinder in die faszinierende Welt der Mathematik zu führen.

Es geht dabei um die Entwicklung des Verständnisses von Zahlen, Mengen, Operationen, Effekten und Phänomenen.

Wir dürfen nicht vergessen, dass die Kinder schon lange bevor sie in den Kindergarten kommen, vielfältige Erfahrungen im mathematischen Gebiet gesammelt haben.

Es ist keine neue Welt, in die man die Kinder führt, deshalb sollten sie von uns mit Natürlichkeit und ohne Angst vor Inkompetenz weiter begleitet werden.

Es ist ja auch selbstverständlich, dass der Kindergarten kein Ort für das mühsame Üben des „Zahlenschreibens“ ist. Dafür ist schon die Schule zuständig. Alles andere kann sich zu einem wunderbaren Abenteuer entwickeln.

Siehe auch:

Mathematische Begabungsförderung

Weitere Projekte zur Mathematik

Grundideen der Mathematik

 

Datum der Veröffentlichung 6.8.09
Copyright © Klaudia Kruszynski 2009, siehe Impressum.

The Advancement of Mathematical Talent in Kindergarten

Posted on by

 

(Lecture at the 4 th IHVO-Symposium, May 5 th , 2007)

by Klaudia Kruszynski

 

This is an account of the project „Time“, which I conducted in the years 2004 and 2005. It was a project for the advancement of mathematical talent of gifted children.

I have been working at a Catholic kindergarten in Münsterland as a supplement kindergarten teacher since 1989, before that I worked at a Polish elementary school. I was well aware of the phenomenon of giftedness at that time and my approach to fostering the talents of gifted children was to instruct them individually, so that the weaker students as well as the stronger students would be taught at their own pace.

 

…in a nutshell…

A comprehensive and multifaceted project demonstrates that mathematics is omnipresent in the children’s world of experience. The mathematics inherent in the project are being explored, which shows how children capture mathematics holistically with all their senses. It is not about pure mathematical training, it is always an approach that addresses different areas of the children’s development simultaneously. Mathematics that come along not as an effort but as play and fun.

The activities to be described here were directed at the in-depth interests of gifted pre-school children.

In order to achieve this goal the following character traits were necessary:

  • Competence and knowledge with regard to the subject.
  • The ability to present this knowledge in an interesting and appealing manner.
  • Equal concern about all students, especially the weaker ones and the gifted students.
  • Creative and unconventional approaches to the subject matters.
  • Curiosity.
  • Open-mindedness.
  • Justice.
  • Humor.

These attributes turned out to be of great value in the effort of advancing gifted pre-school children as well. It was quite exciting for me, and honestly speaking, also rather strenuous to work with these children. Often they were quite annoying, wouldn’t abide by the rules, revolted during morning circles and had fits of fear or anger for no apparent reasons.

Many times I wondered what might be the cause for this conduct. I realised, that these children and their parents as well experienced little sympathy. All children were to be looked at alike and special needs or wishes were not to be granted. This attitude did not seem to be in line with my personal idea of treating the children as individuals. I wanted to help these children, and for that matter myself, too.

Four years ago I attended a symposium conducted by Hanna Vock and immediately signed in for a seminar at her institute. There I met colleagues who understood my concerns and encouraged me to keep lobbying for gifted children.

My Way of Working in Projects

I have learned to observe children closely to find out about their inclinations, abilities and knowledge. Based on these observations I would develop ideas for suitable activities. These were at first designed for children whom I suspected of having special talents. Close observation, conversation and questionnaires on individual interests were then be the basis for the activities. The starting point of such ventures would often be a question raised by the child, a statement given by the child, an observed behaviour or an incidence of some sort.

I learned rather soon that gifted children cannot be advanced separately. They have friends who want to join in, and, of course, other children, too, will show interest in special activities. Singular activities at first, soon developed into full-blown projects which were carried on over longer periods of time and were open to everybody who was interested in participating.

It was my aim to cover the entire spectrum of child development, starting with the just acquired ability to speak in whole sentences, to handle a pen correctly, to show their age by holding up fingers going on to such skills as reading, calculating with numbers exceeding 20 – including multiplication -, pondering life, death and the transitoriness of time …

At the same time the projects were to cover the broad range of childlike interests as they were dinosaurs, planets, automobiles all the way to numbers, books, mechanics and others.

These projects were practical assignments in the course of my further training.

I decided to look at the world from a mathematical point of view together with the children.

With this I meant to pick up on the interest of all children with regard to numbers and their skills in arithmetic. Simultaneously I intended to meet the needs of the gifted children. I meant to help them find answers to their further questions and pick up on their deeper interests.

The project as a whole comprised several subordinate projects which were worked on in different ways:

  • activities for a single child,
  • activities for a part of our group,
  • activities for the whole group or,
  • activities for members of different groups.

The project was designed to address a number of different areas of child development such as: cognition, fine and gross motor skills, speech, thinking. This meant: The range of activities covered the most rudimentary sensory experience as well as purposeful action and even philosophical reasoning.

At this point I would like to describe my way of going about advancing gifted children. These are the essential steps:

  • Determine a possible talent, most of the time one may barely have a hunch that this child might be somewhat different from its peers in age.
  • Spend some time observing – interests, knowledge, inclinations and stage of development.
  • Contemplate suitable activities, which are not exclusively based on the foregoing observations but also on current events, festivities and other projects.
  • Start the project while observing the children and reflecting the observations made. At this stage it is important to also watch the other children and find out whether the project has been arousing the attention of any of them, sometimes they have hidden talents.
  • Enhancement – experiences made, knowledge accumulated and questions raised along the way find their way into the project, a constant updating of the project’s contents.
  • Realisation of further activities, observation and reflexion.

This is how a project may stretch over months, being fed with ever new input, yet never losing its thread.

At this point I will only describe the project at large, because the focus here is on the mathematical contents of the project.

An in-depth discussion of these activities can be found in the article Project Time, right here in the manual. The article also informs you about the methodology I applied in the different activities.

The Project „Time“

In the years 2004 and 2005 I was so lucky as to have more than one talented child in my group. (I cannot speak of giftedness here, since the children had not been tested at the time.)

Among them were two boys: Tim, 5 years, and Jan, 4 years old. They got along great and a wonderful friendship developed between the two. In the course of the project another child joined in, which turned out to be rather talented, too.

Tim was interested especially in cars. He had a deck of cards with all types of cars of different brands and he knew all the manufacturers, the technical data, the top speeds and the prices.

This is how even so early, at the age of 4, he was not only able to read but also to compare numbers of 5 to 6 digits length.

His friend was a tinkerer. He constructed several objects that were supposed to be able to move. He was the most successful at this when working on grandpa’s computer at home. He still tried to do with what we had at kindergarten and built his spaceships, his yet unpractised fingers struggling quite a bit.

Tim and Jan always complained that they never had enough time to spend playing together, the best playing corners were always occupied, when they wanted to play there.

So we tried to find out how that could be. It was a matter of fact: they didn’t have enough time. So I got them a time measuring device, a clock. They usually spent most of their time at the breakfast table. Now every morning they would put the clock on the table before breakfast and then, when they were finished having breakfast, check the time and write it down. And they did so all by themselves, no need for further encouragement or reminding. It was not long before they noticed that these measured time spans differed quite a bit. They also made little drawings of what they had had for breakfast.

They set a time limit for themselves and tried to finish before the timer. That is what caught the other children’s attention. Now many of them wanted to measure the time they took for breakfast and enter the race against the timer. Everybody was given their own sheets of paper to make notes of the measured times and they kept track in writing. One day I brought paper straps with a grid of 270 squares in one row, representing the minutes of the entire morning until lunch. I asked them to colour in the number of squares they had measured and that’s how they saw how those, who had a shorter part of the strap coloured, were earlier off the breakfast table to make a dash for the desired playing corners.

The children used the clock for all kinds of other measurements, too.

How Long Is a Minute?

The first thing we measured was the duration of a song when sung fast or slow. All measurements were made in the unit of “minutes”.

But then, how long is a minute really?

The children were to keep their eyes closed for what they thought was a minute. After a few seconds some of them opened their eyes. Too early!

So they tried again. It wasn’t easy, we used the timer.

They watched the numbers change, getting smaller and smaller. Upon zero the alarm went off.

Then they went on to measure other activities, for example how long it takes to read a picture book. We set off the timer and … all of a sudden Tim started reading the book out loud. With some effort, spelling out the longer words to himself first, he struggled through the book. It took him about nine minutes.

We were speechless, none of us was aware, he could read. His younger friend said sadly, he really wished he too could read.

These activities comprised the following mathematical contents:

  • Perceiving the duration of one minute
  • Estimating the duration of one minute
  • Grasping the notion of “amount” (here: of time) in numbers (here: of minutes)
  • Conceiving of numbers as signifying position / order
  • The growing of numbers
  • Minutes as a unit for the measurement of time
  • A minute as the equivalent of 60 seconds
  • A minute as 1/60 of an hour
  • Sensing rhythm and tempo
  • Handling of a clock

The gifted children were pursuing the whole issue with much more zeal. They would ask questions, look for answers themselves, experiment and implement their newly acquired knowledge in their games. For example, when they were playing “spaceport” they would start their rockets with a countdown, certainly starting no lower than at 20.

Advancement of gifted children:

Understanding of a minute as a unit for the measurement of time

Comparing the analogue and the digital method of time measurement

Elaborating on the way a countdown works and using it

Estimating the duration of different activities

Performing different measurements and taking down the results

Seconds, hours and other units of time measurement

Ever since that day our clock has not been resting in its place; measurements had to be taken, alarms went off, more and more children hooked on to the topic.

At the Gym

When all children had learned to handle the clock and write down times, they decided to take the clock to the gym.

As ‘time detectives’ they measured time, wrote it down, gave instructions and all the while got an idea how difficult it is to keep a grip on the group.

For the gymnastic game we distributed animal symbols: snail, hedgehog, hare. There were little cards with animal symbols on them that were distributed randomly among the children later on.

Mathematical contents:

  • Measuring time
  • Writing down time
  • Comparing results
  • Different speeds: slow, moderate, fast
  • Matching the speeds with the animals
  • Combining speeds and distances
  • Deliberately moving at specific speeds
  • Different distances: near and far
  • Comparing the measured times

I would like to use this activity as an example by which to demonstrate to you how I went about laying mathematical groundwork with the children. As you are aware children need sensory experience in order to later on be able to perform abstract operations.

Even before they can count they are able to experience amounts in the sense of magnitudes by their own actions. They notice when they make more steps or that they are running faster. They feel their breath, feel that their legs getting tired. They experience the change in place when moving, they see the distance they have covered. At first they move spontaneously and at random, but with time their moves become more targeted and controlled by their will.

At the same time children grow aware that the world, too, moves around them: everybody else, animals, vehicles. Here too, children recognize different speeds and they experience them in connection with different distances covered.

That is how they know that a snail is very slow and needs a lot of time to cover a distance. The hedgehog does much better and the hare is the fastest.

By imitating the animals the children learn to change their speed intentionally. They also experience how as a snail it takes them forever to make it to the other side of the gym.

The gifted children have long been able to recognize speeds and match them with the right animals. Their task is much more abstract and complex, and allows for no more making use of their own physical sensations; they have to rely solely on their experience and knowledge. In this game they are to pick one child from the crowd, watch it for a while and match it with the animal symbol. They can even count the many steps, measure the time, write it down and compare it.

Advancement of gifted children:

Measuring time and writing it down

Comparing results

Coming up with ideas and suggestions

Sundial

Well, the story of time wasn‘t all told, it seemed, it unraveled and revealed some more. The question, how we know what time it is, was quickly answered – we see it on the clock. But how does the clock know? Or: what happens if there is no clock? This was getting tricky. I got some books about time and about clocks. From these books the children learned how time was measured in former times. The sundial mystified them.

It was surprisingly simple to build a sundial, all you needed was a stick. Somehow the children also knew that the sun was involved, because the stick’s shadow served as the ‘clock’s hand’. On a sunny morning they went outside into the yard and stuck a stick between the stone slabs. The sundial was operational at once – just, what time was it showing?

Mathematical contents:

  • Realisation of the changes in the position and the length of the shadow
  • Relation: sun + stick = shadow
  • No sun: no shadow
  • Motion of the sun – time passing
  • Thinking ahead
  • Drawing conclusions
  • Writing down time

In this project all children were able to understand practically a mathematical relation:
sun + stick in the ground = shadow, and they could experience what happens if one part of the equation is missing.

They understood that the moving of the shadow meant a change in time.

The gifted children understood the way the sundial worked so well that they were able to estimate the position of the shadow, even when the sun was not shining or where it would be at later point in time. They also recognized the down sides of measuring time this way.

Advancement of gifted children:

Understanding the working principle of a sundial

Looking for a good place for the sundial

Systematic observation

Writing down times

Anticipating changes

Reporting, telling the other children how the sundial works

Comparing the performance of a sundial with that of other kinds of clocks

Drawing conclusions

That’s how they came to understand that a sundial is not a reliable way of telling the time.
Therefore we decided to use modern clocks to measure time.

Engineering a clock

How does a clock work?

That is a question some children will raise. When taking an old alarm clock apart, all kinds of axles and wheels emerge, when you shake the clock they move. But they are much too delicate for little children’s hands.

From a mail-order catalogue I ordered an alarm clock kit. The parts were made of plastic, big enough, and I was confident this would be great fun for my “tinkerer”.

One afternoon the time had come to put it together. He unpacked all parts and checked if the kit was complete. He examined each part and then unfolded the manual. He proceeded quite systematically and with great patience he put the parts together, step by step. Then he closed the case, wound the clock and waited. The clock worked for a few seconds then it stood still. So he took it apart and reassembled it, meticulously following the manual. With great confidence he wound the clock again, but with the same result. He took it home to ask his grandfather for help.

However, what was positive even about this failed attempt was: the boy was able to conceptualize exactly how the parts fit together, how the wheels and pinions would mesh, how they would drive the hands and what the pendulum was good for. He showed great patience, wanted to solve the problem himself, checked his procedure several times and knew where he could get help.

What is the mathematics in assembling a clock? That’s what some might ask. The numbers on the face, the gear teeth on the wheels, different speeds of the wheels, these are mathematical contents of this activity.

Further mathematical contents are:

  • Matching parts and sketches in the manual
  • Comparing the number of teeth with the size if the wheels
  • Understanding a manual and the necessity of doing things in the right order
  • Different rotational speeds of the different size wheels

Gifted children are able to understand the manual, to follow its instructions and come up with the right results. They are not discouraged by set-backs, but try to find the causes for failures and try again. They understand the interplay of the gear wheels and explain the way a clock works to other children.

Advancement of gifted children:

Reading the manual

Organizing the work

Quality check

Explaining the way it works

Understanding mechanics – why do the hands move?

Art-Project

One day I brought my collection of clocks to kindergarten. I spread them on a blanket and we listened to the Pink Floyd CD with the song “Time” on it. On the wall we had the famous Salvador Dali painting “The Persistence of Memory” with the dangling watches.

I gave the children some time to look around and appreciate everything around them. They held the clocks to their ears, turned the little wheels.

This is some of the „philosophical discourse“ with the children:

„What do the clocks feel like?“

“Solid, cold, hard.”

“Does time feel hard, too?”

“Time isn’t hard, it’s soft.”

“Can time be held in the hand?”

“No …”, everybody was laughing, one boy made circular motions and said “Time always goes like this.”

“True, there was a painter who thought the same way, that time couldn’t be held in the hand because it always moves on and he painted it in his picture.”

So the children looked at the picture.

What on the picture is hard?”

“The mountains, the table, the tree…, no, the tree isn’t hard, it looks dead, but if the clock goes on ticking, spring will come and the tree lives again.”

“And what on the picture is soft?“

“The watches, they’re showing the time, and it is not dead, it’s always moving on.”

The children had really understood the nature of time, they now also distinguished between time and the instrument for measuring it, the clock; a difference that at the onset of the project was not all that clear.

We decided to paint our own copies of the picture by Salvador Dali.

This project was open to all children of the group. Everybody contributed their skills and knowledge. For some of the children it was quite an achievement to read the time on the clock and understand its use to measure time. Others were able to align the numbers in the order of their value. Along the way they realized that the hands on the clock keep covering the same ‘route’ over and over again, that after two rounds a new day begins and that this never ends because time itself keeps moving on and doesn’t end either. Just like a circle doesn’t have a beginning or an end.

The children all experienced several different sensory inputs. They felt how hard the surface of a clock was and how soft the putty, they listened to music, looked at the painting by Salvador Dali, mixed up the colours when painting themselves, made use of different materials for their handicraft works.

 

The gifted children recognized the meaning of time through their sensory experiences – its soft and ever moving nature. They realized that something in that motion is repetitive, yet at the same time changes, that the tree will have leaves again and again when spring comes around, but that after many years that tree will die. Just like it is with people.

What feels hard, though, doesn’t change, isn’t alive, like the clocks and the mountains. Their time can become “infinite”.

Mathematical contents:

  • Perception of the transitoriness of time
  • Perception of the changes rendered in time
  • Rate of change: fast, slow, „no“ change
  • Matching speeds and objects: the clock ticks fast, the tree changes in a yearly cycle, the mountains don’t seem to change at all
  • The circle as an appropriate geometric form to represent time – the hands moving in a circle, at different paces
  • Configuration of a clock
  • Numbers
  • Meaning of numbers on a clock face
  • Crafting / shaping numbers
  • Correct order of numbers on the clock face

Advancement of gifted children:

Active participation in the discussion

Recognizing of states and processes

Developing own ideas

Trying to explain: What was the basic idea here?

Fine motor skills trained (putty)

Participation in creative activities

Explaining, reporting to an audience

The finished painting was exhibited, displayed in a special place in the room and explained to the parents by the artists.

 

Brushing Teeth

In this project we were dealing with algorithms. The term algorithm is pivotal in mathematics. See also: Basic Ideas of Mathematics . Its meaning is: a sequence of instructions (steps) which define a procedure, beginning with the input of certain data and always rendering a definite result. Any purposeful activity can be broken down into its algorithmic steps. For example: brushing teeth.

On day I asked some of the children: „What are all the things that need to be done to clean one’s teeth?” I got all kinds of answers, quite a jumble.

“How are you going to explain it to somebody, who has never brushed his teeth before?”

So we imagined we were in the bathroom wanting to brush our teeth.

I starts with getting the mug. Then fill it with water and rinse the mouth. Next thing open the toothpaste, put some on the brush, brush the teeth: from all sides, back and forth, circling motions, spitting and rinsing the mouth again. Clean the mug and the brush, put them back, dry the mouth, done.

Mathematical contents:

  • Algorithms
  • Recognizing single steps in a complex procedure
  • Correct order of steps leads to success
  • Every single step is necessary in order to succeed

Advancement of gifted children:

Defining a sequence:

Cause -> status -> action -> effect

Defining the course of actions in a complex activity

Deliberations: „What happens if I skip one part in the sequence?“

Deliberations: „What happens if I change the order?“

Algorithms regulate the proceedings and lead us safely to the end if we take all steps in the correct order. Mathematical operations are algorithms, too. One of the most elementary is: how to write a number; later: how to add or perform other operations, how to figure out an unknown value or how to determine the equation of a function.

The gifted children had great fun determining different algorithms. We called them recipes. For the “brushing teeth recipe” we created a sequence of photographs. We glued the pictures on a strap and hung it up on the wall in the bathroom.

Growing Beans

Around the turn of the year the children sing a lot of songs, and one is especially popular – it is called “The Yearly Clock”, with all the months in their correct order, and then it all starts all over again!

This is how the children understand that time can be measured, for example, human life or the life of plants. Human life can be rather long, even the children know that, but the life of a bean plant can easily be measured.

So we started a gardening project. The children exposed the bean seeds to different conditions:

  • In the water / without water
  • In an open bowl / in the dark in a jar
  • In the soil / without soil
  • In an open container / in a closed container

The beans were being observed from day to day, one child documented the changes in a table, and at the end the beans were photographed with a number to show how many days the experiment was going on. This is how the children saw life develop in time, and waste away again.

When the beans were reaped, the children made a diagram showing how many “baby beans” one “mother bean” had. For this every child was examining one plant. Then we dared to predict how many “grandchildren beans” we would get next year.

But we didn’t wait that long, we made a picture book about a dwarf, who wanted to invite his friends for a bean stew in autumn. We did some cooking ourselves, too, that’s how the beans ended up in our stomachs.

In this project the children did not only see the growth of beans but also growing numbers.

In their daily documentations they laid the number corresponding to the day of the experiment next to the documented objects. It started with “1” and the next day it was the “2” and the “3” on the third day and so on until the day of the harvest.

It was really exciting when the number went beyond ten – how do you write “11”? Then the next obstacle. How do you write “21”? „1“ and then „2“ or the other way around? Some children knew exactly how to write the big numbers, the others learned from them and had their own suggestions to make. They understood that the number is written “backwards”.

[Note from the translator: In Germany, two-digit numbers are written just as anywhere else: from left to right with the tens in the first position and the units in the next position to the right. However, they are spoken backwards, so that 21 is spoken one-and-twenty (einundzwanzig) in German. Since the children learn to speak the numbers before they write them, they think they speak them in the normal order, consequently the way the numbers are written will then appear “backwards” to them.]

And there was another kind of growing numbers the children got to see just after the harvest. From one bean came 15 “baby beans”. If we planted them next year we would get 15 times 15 “grandchildren beans”, and if we did the same thing the following year we would have 15 times 15 times 15 “great-grandchildren beans”. The gifted children tried to figure that number. I suggested they make a drawing of it. That was a great many beans. This way one could acumulate riches over the years. But who wants to eat beans all the time?

What do you do with all those beans? You could trade them for something else, for example for potatoes or carrots. You could sell the beans and buy some clothes.

This is how the gifted children understood how the economy works. Same thing with the crop: the farmer can sell the crop he doesn’t need for himself and buy other things for the money.

Mathematical contents:

  • Perception of change in time / growth / death
  • Writing numbers in ascending order
  • Change of amounts
  • Adding up (bean-children)
  • Powers – and the phenomenon of „multiplication“
  • Exchange / trade / price
  • Prediction of future results based on experience

Advancement of gifted children:

Documentation of the experiment

Completing observation forms

Responsibility for the progress of the experiment

Counting great numbers / amounts

Adding and subtracting and their notation

Coordinating activities in creating the picture book

Understanding food production and agriculture

Understanding trade as a form of exchange

Understanding commercial ties

Time-Roll

The many activities and talks about time also raised the question how long time goes back, when did it begin? Jan had the answer: with the big bang. B illions of years ago. And how long ago was this?

In order to demonstrate this to the children I used a roll of wallpaper about 20 meters long and rolled up.

In the middle of it there wasn’t anything on the paper, just like at the beginning of the universe. The solid core was dark, it was the big bang. Then I coloured the upper end of the paper roll starting with red in the middle, going to orange, yellow and finally green. Our space expert got the idea and explained to the other children: At the beginning there was nothingness, then there was an explosion, the stars and the planets formed, and everything was still very hot, it cooled down and when the earth turned green it was because of the plants and the animals. And, of course, not the kinds we see today, but dinosaurs. But it was a long time ago and they are extinct now.

The children knew this already.

So the other end of the roll is today. When you unravel the roll you go backwards in time until you get to dinosaur-time. That’s what we did, some children drew a few dinos, others looked through books on the history of earth. A few days later there were quite e few dinos inhabiting the time-roll.

In this project it was the gifted children who explained time to the others. It was incredible how much the children knew about this. Especially Jan understood how matter came to life. He knew that it had taken billions of years until earth had cooled down so that the first plants and animals could populate it. He was able to measure time another way, namely by the most important occurrences.

This is how he aroused everybody else‘s interest in the history of earth.

He sought for validation of his knowledge and I reassured him. He brought books for the group, in which one could view the emergence of life. Only shortly before the end the children discovered the first human beings.

In those times earth looked different. There were no houses, no streets nor cars and the people were wearing clothes made out of fur. They learned to light a fire, ate cooked meat for the first time. How many generations have lived until people lived the way we do today?

All of a sudden the children realized that there are very big numbers, they couldn’t name them, but by examining history they got an idea of their order of magnitude. They know that time moves on, nobody knows how long this will go on, so time is endless, growing with every second, minute, with every year.

Time moves only in one direction, but it is possible to think the past – one can’t hunt dinosaurs, but one can draw them on the time-roll.

Time and time again the children went to get the time-roll and made drawings on it. If they wanted to draw dinosaurs, they had to unroll it quite far. For the first locomotive not so far, even less for cars. One of the last inventions of mankind, the mobile phone, would have to be drawn at the open end of the roll.

Mathematical contents:

  • Endlessness of time
  • Past, present, future
  • Moving in time: forwards and backwards
  • Time units: second, minute, hour, day, month, year, decade, era
  • Rate of change – ever faster
  • Number of changes – ever more
  • A feel for the relativity of the length of a human life

Advancement of gifted children:

Contributing knowledge of the phenomenon of time

Contributing knowledge of the universe

Contributing knowledge about the history of earth

Understanding of large numbers

Understanding changes in time

Understanding the irreversibility of time

Understanding the laws of nature

This project lasted many months.

It took its time to understand time. The only way was, of course, experiencing a chain of many events.

In order to understand the passing of time one can document the events and remember them later when looking at them.

Any topic is fit to show the different kinds of talents the children have and to promote them. Any topic allows for a number of different activities, which address several domains of child development.

Addressing several senses at the same time strengthens focus, elongates the time span of concentration and creates a special atmosphere that promotes motivation.

By embracing the individual talents and strengths the individual’s sense of affiliation with the group is intensified. The group profits from the talents of the individual and is stimulated in its development.

  • Mathematical advancement is present in all areas of the work with children at kindergarten.
  • Activities do not have to emphasize formal aspects as taught in school.
  • It starts with the most simple functions like sorting, matching pairs and may be expanded indefinitely. The skills and interests of the children will determine how far they want to take it (understanding amounts, reading numbers, writing numbers, doing arithmetic).
  • Mathematical advancement will be especially successful if all senses are addressed, including motion.

There is no necessity for a special training in mathematics in order to advance gifted pre-school children; however, important are:

  • Attentiveness,
  • a sense of rhythm and order,
  • enjoying doing arithmetic,
  • playful approach to numbers and mathematical operations,
  • creativity,
  • courage to do new things,
  • exchanging ideas with the colleagues,
  • looking at the available games from a mathematical point of view,
  • positive reinforcement of the children’s knowledge and interests,
  • working in small groups of children with the same interests and skills.
For us kindergarten teachers any occasion can be used to guide the children into the fascinating world of mathematics.

It is all about developing an understanding of numbers, amounts, operations, effects and phenomena.

We must not forget that the children have gathered mathematical experience long before they enter kindergarten.

It is not a new world which the children are introduced to, therefore they should be accompanied by us with ease and without fear of one’s own incompetence. It is quite obvious that kindergarten is not a place of tedious drill in “writing numbers”, that school’s business.

Anything else can lead to a fascinating adventure.

Date of publication in German: May 5th, 2007
Translated by Arno Zucknick
Copyright © Klaudia Kruszynski, see Imprint.

Mathematische Begabungsförderung im Kindergarten

Posted on by

Vortrag bei der 4. IHVO-Fachtagung am 5.5.07

von Klaudia Kruszynski

 

Dies ist ein Bericht über das Projekt „Zeit“, das ich in meinem Kindergarten in den Jahren 2004 und 2005 durchgeführt habe.

Es handelt sich um mathematische Förderung hoch begabter Vorschulkinder.

Seit 1989 arbeite ich in einem katholischen Kindergarten im Münsterland als Ergänzungskraft, früher arbeitete ich an einer Grundschule in Polen. Das Thema „Hochbegabung“ war mir damals schon bekannt. Mein Weg, die hoch begabten Kinder zu fördern, war der individuelle Unterricht. Es bedeutete, dass jeder Schüler, besonders der leistungsschwache und auch der begabte entsprechend gefördert wurde.

 

…kurz gefasst…

Am Beispiel eines umfangreichen und vielfältigen Projekts wird gezeigt, dass Mathematik in der alltäglichen Umwelt der Kinder vorhanden ist. Es werden die mathematischen Anteile in dem Projekt herausgearbeitet, wobei deutlich wird, dass die Kinder die Mathematik mit allen Sinnen und ganzheitlich erfassen.
Es geht nicht um ein isoliertes mathematisches Lernen, sondern um eine Förderung, die immer mehrere Entwicklungsbereiche anspricht. Mathematik nicht als Mühsal, sondern als Spiel und Spaß. Deshalb sollten sich auch Erzieherinnen verstärkt an die Mathematik heran trauen.

Die beschriebenen Angebote wurden auf die vertieften und weitergehenden Interessen und Fähigkeiten hoch begabter Vorschulkinder ausgerichtet.

Um dieses Ziel zu erreichen, waren die folgenden Eigenschaften unentbehrlich:

  • Kompetenz und Wissen im und um das Fach.
  • Fähigkeit, das Wissen interessant und ansprechend zu vermitteln.
  • Sorge um jeden Schüler, besonders um den leistungsschwachen und den begabten.
  • Kreativer und unkonventioneller Umgang mit dem Unterrichtsstoff.
  • Neugier.
  • Aufgeschlossenheit.
  • Gerechtigkeit.
  • Humor.

Diese Eigenschaften waren, wie es sich herausstellte, auch sehr hilfreich bei der Förderung hoch begabter Vorschulkinder. Es war für mich sehr spannend und, ehrlich gesagt, anstrengend, mit diesen Kindern zu arbeiten. Sie sind oft sehr negativ aufgefallen, weil sie sich an die Gruppenregeln nicht halten wollten, im Stuhlkreis rebellierten, scheinbar unbegründete Angst oder Wutausbrüche hatten.

Oft habe ich mich nach dem Grund für dieses Verhalten gefragt. Ich merkte, dass diesen Kindern und ihren Eltern wenig Verständnis entgegen gebracht wurde. Alle Kinder sollten mit gleichem Maß betrachtet werden, und es sollte nicht auf besondere Wünsche eingegangen werden. Diese Haltung passte nicht zu meinem persönlichen Ziel, jedes Kind individuell zu betrachten. Ich wollte diesen Kindern helfen. Auch mir selbst.

Vor vier Jahren habe ich an einer Tagung teilgenommen, die Hanna Vock durchgeführt hat, und habe mich danach sofort für die zweijährige Weiterbildung an ihrem Institut angemeldet. Dort habe ich Kolleginnen getroffen, die meine Sorgen verstanden und mich ermutigt haben, mich weiter für hoch begabte Kinder einzusetzen.

Meine Projekt-Arbeitsweise

Ich habe gelernt, Kinder gezielt zu beobachten, um ihre Fähigkeiten, Kenntnisse und Interessen herauszufinden. Auf dieser Basis überlegte ich mir entsprechende Angebote. Sie waren zuerst für die Kinder konzipiert, bei denen ich besondere Begabungen vermutete. Eine längere Beobachtung, Gespräche, Interessenfragebögen bildeten die Grundlage des Angebots. Als Anlass galt meistens eine Frage, Aussage oder ein bestimmtes Verhalten des beobachteten Kindes. Oder ein Ereignis.

Sehr schnell habe ich begriffen, dass man die Hochbegabten nicht gesondert fördern kann. Sie hatten Freunde, die mitmachen wollten, und natürlich interessierten sich auch andere Kinder für diese Angebote. Aus einzelnen Angeboten entwickelten sich größere Projekte, die über einen längeren Zeitraum gelaufen sind und allen Interessierten zugänglich waren.

Mein Ziel war es, das breite Spektrum der kindlichen Entwicklung zu berücksichtigen, von gerade erworbenen Fähigkeiten, in Sätzen zu sprechen, den Stift geschickt führen zu können, das eigene Alter mit Hilfe der Finger zu zeigen usw. bis zum eigenständig Lesen können, Rechnen über 20 – Multiplizieren eingeschlossen -, über das Leben, den Tod und die Vergänglichkeit der Zeit nachzudenken, usw.

Gleichzeitig sollten die Projekte das breite Spektrum der kindlichen Interessen und Kenntnisse beinhalten, von Dinosauriern, Planeten, Autos bis hin zu Zahlen, Büchern, Mechanik, usw.

Diese Projekte waren Praxisaufgaben bei der Weiterbildung.

Ich habe mich entschieden, die Welt zusammen mit den Kindern aus einer mathematischen Sichtweise zu betrachten.

Dadurch wollte ich die wachsenden Interessen aller Kinder an Zahlen und Fertigkeiten beim Rechnen aufgreifen. Gleichzeitig beabsichtigte ich, den hoch begabten Kindern gerecht zu werden. Ich wollte ihnen helfen, Antworten auf ihre weitergehenden Fragen zu finden, und ihre tiefer gehenden Interessen aufgreifen.

Das Gesamtprojekt umfasst mehrere Teilprojekte, die in unterschiedlicher Form abliefen, und zwar als

  • Einzelangebote,
  • Kleingruppenangebote,
  • Großgruppenangebote oder als
  • Gruppen übergreifende Angebote.

Das Projekt wurde so angelegt, dass viele Bereiche der kindlichen Entwicklung angesprochen waren: Wahrnehmung, Feinmotorik, Bewegung (Grobmotorik), Sprache, Denken. Das bedeutete: Die Spanne der Angebote reichte von einfachsten Sinneserfahrungen über gezieltes Tun bis zum philosophischen Nachdenken.

Ich möchte an dieser Stelle meine Vorgehensweise der Hochbegabtenförderung beschreiben. Dabei sind folgende Schritte zu erkennen:

  • Feststellung (Entdeckung) der möglichen Begabung, wobei man meistens nur ein Gefühl hat, dass das Kind anders ist als die meisten Kinder in seinem Alter.
  • Zeit der Beobachtung – seiner Interessen, Kenntnisse, Vorlieben, seines Wissens und Entwicklungsstandes.
  • Überlegung passender Angebote, wobei nicht nur die Erkenntnisse aus der Beobachtung die Grundlage bilden, sondern auch das aktuelle Geschehen, Feste und Gruppen übergreifende Projekte.
  • Durchführung des Angebots mit gleichzeitiger Beobachtung der Kinder und einer Reflexion. An dieser Stelle schaut man, ob das Angebot auch das Interesse anderer Kinder weckte – auch die sollten genauer beobachtet werden, weil oft unerkannte Begabungen in ihnen stecken können.
  • Weiterentwicklung – die Erfahrungen, gesammelten Kenntnisse, entstandenen Fragen usw. werden berücksichtigt.
  • Durchführung neuer Angebote, Beobachtung, Reflexion.

So kann es passieren, dass ein Projekt sich über Monate hinzieht, ständig neue Inhalte bekommt, aber immer den Leitfaden behält.

Die ausführliche Darstellung der Angebote können Sie im Beitrag Projekt Zeit hier im Online-Handbuch nachlesen. Dort erfahren Sie auch etwas darüber, wie ich die Projekte methodisch angelegt habe.

An dieser Stelle beschreibe ich die Projekte nur knapp, weil es hier darauf ankommen soll, die mathematischen Inhalte des Projekts herauszuarbeiten.

Das Projekt „Zeit“

In den Jahren 2004 und 2005 hatte ich das Glück, mehr als ein besonders begabtes Kind in der Gruppe zu haben. (Ich kann hier nicht von Hochbegabung sprechen, weil diese Kinder zu dieser Zeit nicht getestet waren.)

Dazu gehörten zwei Jungen, Tim, 5 Jahre und Jan, 4 Jahre alt. Sie verstanden sich sehr gut, es entwickelte sich eine wunderschöne Freundschaft zwischen den Beiden. Im Laufe des Projekts kam noch ein weiteres Kind dazu, bei dem sich eine hohe Begabung herausstellte.

Tim interessierte sich besonders für Autos. Er hatte eine Sammlung Karten mit verschiedensten Automarken, wusste den Hersteller, die technischen Parameter, die Höchstgeschwindigkeit und den Preis.

So konnte er mit vier Jahren die fünf- und sechs-stelligen Zahlen nicht nur lesen, sondern auch vergleichen.

Sein Freund Jan war ein Tüftler. Er baute unterschiedliche Objekte, die sich bewegen sollten. Am besten klappte es an Opas Computer, trotzdem versuchte er aus dem Vorhandenen auch im Kindergarten seine Raumschiffe zu bauen, wobei seine ungeübten Finger noch sehr viel Mühe damit hatten.

Tim und Jan beschwerten sich ständig, dass sie nie genug Zeit zum Spielen hätten, die besten Spielecken wären schon immer belegt, wenn sie darin spielen wollten.

Also haben wir angefangen zu schauen, was die Ursache wäre. Die Tatsache war klar – ihnen fehlte Zeit. Also besorgte ich einen Zeitmesser, eine Uhr. Die meiste Zeit verbrachten sie am Frühstückstisch. Sie haben jeden Tag selbstständig die Uhr zu Beginn des Frühstücks aufgestellt und am Ende die Zeitdauer auf einem Blatt aufgeschrieben. Sie merkten schnell, dass es sehr unterschiedlich sein konnte. Sie malten auf dem Blatt auch auf, was sie zu essen hatten.

Sie setzten sich ein Zeitlimit und versuchten, schneller als der Timer zu werden. So wurden die anderen Kinder auf das Geschehen aufmerksam. Und dann wollten viele ihre Frühstückszeit messen und mit dem Timer um die Wette eilen. Auch sie bekamen ihre Mess-Blätter und schrieben ihre Ergebnisse darauf. Eines Tages brachte ich Streifen mit 270 Kästchen mit – für die gesamte Vormittagszeit von viereinhalb Stunden – und regte die Jungen an, so viele auszumalen, wie viele Minuten sie zum Frühstücken gebraucht haben. Und so bekamen sie ihre Antwort.

Die Uhr wurde von den Kindern auch zu anderen Messungen genutzt.

Erstens: Wie lange dauert eine Minute?

Das erste, was wir gemessen haben, war die Dauer eines Liedes, mal schnell mal sehr langsam gesungen. Alle Ergebnisse waren in Minuten.

Aber wie lang ist denn eine Minute?

Die Kinder sollten die Augen so lange geschlossen halten, wie sie glaubten, dass eine Minute dauern würde. Schon nach ein paar Sekunden öffneten die ersten ihre Augen wieder. Zu früh!

Also versuchten sie es noch mal. Es war nicht einfach, wir benutzten den Timer.

Sie beobachteten, wie die Zahlen sich veränderten – wie sie immer kleiner wurden. Und bei Null klingelte es.

Danach wurden andere Tätigkeiten bemessen, unter anderen wie lange man für ein Bilderbuch braucht. Wir starteten die Uhr und… da fing Tim an, das Buch zu lesen. Mit ein wenig Mühe, die längeren Wörter buchstabierend, kämpfte er sich durch das Buch. Nach etwa neun Minuten war er fertig.

Wir alle waren sprachlos, keiner hatte gewusst, dass er schon lesen konnte. Sein jüngerer Freund sagte traurig, er würde auch so gerne lesen können.

In diesem Angebot wurden folgende mathematische Inhalte berücksichtigt:

  • Wahrnehmen der Dauer einer Minute
  • Schätzen der Dauer einer Minute
  • Begreifen der Zahl als Menge
  • Begreifen der Zahl als Position/Reihenfolge
  • Wachsen der Zahlen
  • Minute als Einheit zum Zeitmessen
  • Minute als 60 Sekunden
  • Minute als 1/60 einer Stunde
  • Erspüren des Rhythmus und der Geschwindigkeit
  • Bedienung einer Uhr

Die hoch begabten Kinder beschäftigten sich mit diesen Inhalten weit intensiver. Sie stellten Fragen, suchten selber nach Antworten, experimentierten, bauten ihr neu erworbenes Wissen in ihre Spiele ein. Zum Beispiel: Als sie Raumhafen spielten, starteten ihre Raketen nach einem Countdown, natürlich mindestens bei 20 angefangen.

Hochbegabtenförderung:

 

– Begreifen der Minute als Maßeinheit

– Vergleichen der analogen und digitalen Methoden der Zeitmessung

– Erklären des Funktionierens und Verwendung des Countdowns

– Schätzen der Dauer verschiedener Tätigkeiten

– Verschiedener Messungen und Aufschreiben der Ergebnisse

– Sekunde, Stunde und andere Einheiten der Zeitmessung

Seit diesem Tag blieb unsere Uhr nicht mehr am Platz stehen; es wurde gemessen, geklingelt, immer mehr Kinder interessierten sich für das Thema.

Zweitens: Turnangebot

Als die Kinder gelernt hatten, mit der Uhr umzugehen und die Zeiten aufzuschreiben, beschlossen sie, die Uhr zum Turnen mitzunehmen.

Als Zeitdetektive haben sie die Zeit gemessen, aufgeschrieben, Kommandos gegeben. Nebenbei merkten sie, dass es nicht einfach ist, in der Gruppe für die nötige Ordnung und Ruhe zu sorgen.

Beim Turnen wurden Karten mit Tiersymbolen: Schnecke, Igel, Hase genutzt. Es gab auch kleine Kärtchen mit den Tiersymbolen, die die Kinder später nach dem Zufall zugeteilt bekamen.

Mathematische Inhalte:

  • Zeit Messen
  • Aufschreiben der Zeiten
  • Vergleichen der Zeiten
  • Verschiedene Geschwindigkeiten: langsam, mittel, schnell
  • Zuordnen der Geschwindigkeiten zu den Tieren: Schnecke, Igel, Hase
  • Bewusstes Bewegen in unterschiedlichen Geschwindigkeiten
  • Verschiedene Entfernungen: nah, weit
  • Kombinieren von Geschwindigkeiten und Entfernungen
  • Vergleichen der gemessenen Zeiten

Bei diesem Angebot würde ich Ihnen gerne zeigen, wie ich durch Bewegung mathematische Grundlagen entwickele. Wie Ihnen bekannt ist, brauchen Kinder konkrete Erfahrungen, damit sie später in ihren Gedanken abstrakte Operationen durchführen können.

Schon bevor sie zählen können, sind sie in der Lage, die Mengen durch ihr Tun zu erfahren. Sie spüren es, dass sie mehrere Schritte machen oder dass sie schneller laufen. Sie merken es an ihrem Atem, spüren, dass die Beine müde geworden sind. Sie erfahren, wie sie durch ihr Bewegen den Platz wechseln, sie sehen, welche Strecke sie bewältigt haben. Am Anfang ist die Bewegung spontan und eher zufällig, aber mit der Zeit wird sie zielgerichtet und durch den Willen gesteuert.

Gleichzeitig lernen Kinder, dass sich auch die Welt um sie herum bewegt: die anderen Menschen, Tiere, Fahrzeuge. Auch hier erkennen Kinder verschiedene Geschwindigkeiten und erfahren, dass es sich dabei um verschiedene Entfernungen handeln kann.

So wissen sie, dass eine Schnecke sehr langsam ist und viel Zeit braucht, um eine Entfernung zu bewältigen. Der Igel ist schneller und der Hase am schnellsten.

Durch das Nachahmen der Tiere lernen Kinder bewusst die Geschwindigkeit zu wechseln. Sie erfahren auch, dass sie als Schnecke sehr lange brauchen, um auf die andere Seite der Turnhalle zu kommen.

Die hoch begabten Kinder sind schon früher in der Lage, die Geschwindigkeiten zu erkennen und den Tiersymbolen zuzuordnen. Ihre Aufgabe ist viel abstrakter und komplexer. Sie orientieren sich nicht mehr am eigenen Körperbefinden, sondern nutzen ihre Erfahrungen und ihr Wissen. Bei dem Spiel müssen sie sich zuerst ein Kind aus der Menge aussuchen, es eine Weile beobachten und schnell dem Tierkärtchen zuordnen. Sie können auch schon die vielen Schritte zählen, die Zeit messen, aufschreiben und vergleichen.

 

Hochbegabtenförderung:

– Zeit messen und aufschreiben

– Vergleichen der Ergebnisse

– Entwickeln eigener Ideen, Vorschläge

Drittens: Sonnenuhr

Aber die Geschichte von der Zeit entwickelte sich weiter. Die Frage, woher man weiß, wie spät es ist, wurde schnell beantwortet – von der Uhr. Aber woher die Uhr es weiß, oder was dann ist, wenn man keine Uhr dabei hat, das war schon nicht so einfach zu beantworten. Ich besorgte Bücher über die Zeit und über Uhren. Daraus erfuhren die Kinder, wie man in früheren Zeiten die Zeit gemessen hat. Besonders interessant war die Sonnenuhr.

Es war erstaunlich einfach, eine Sonnenuhr zu bauen, man brauchte dafür nur einen Stock. Aus dem Buch wussten die Kinder, dass man auch die Sonne dazu braucht, weil der Schatten der Zeiger ist. An einem sonnigen Vormittag gingen sie in den Garten und steckten einen Stock zwischen Steinplatten. Die Uhr funktionierte sofort. Nur, wie spät war es eigentlich?

Mathematische Inhalte:

  • Wahrnehmung der Veränderungen der Position und der Länge des Schattens
  • Relation: Sonne + Stock in der Erde = Schatten /
    Keine Sonne: kein Schatten
  • Bewegung der Sonne – Zeitvergehen
  • Vorausdenken
  • Schlüsse ziehen
  • Zeit aufschreiben

Bei diesem Projekt konnten alle Kinder eine mathematische Relation praktisch begreifen: Sonne + Stock in der Erde = Schatten und erfahren, was passiert, wenn ein Teil der Relation nicht mehr vorhanden ist.

Sie verstanden, dass die Wanderung des Schattens eine Zeitveränderung bedeutet.

Die hoch begabten Kinder konnten das Funktionieren der Sonnenuhr so gut nachvollziehen, dass sie in der Lage waren, die Position des Schattens zu schätzen – auch ohne die Sonne oder zu späteren Zeitpunkten. Sie erkannten auch die Nachteile dieser Art, Zeit zu messen.

Hochbegabtenförderung:

– Erkennen des Prinzips, wie eine Uhr funktioniert
– Suchen einer geeigneten Stelle für die Sonnenuhr
– Systematische Beobachtung
– Schreiben der Uhrzeiten
– Voraussehen der Veränderung
– Berichten, anderen Kindern erzählen, wie die Uhr funktioniert
– Vergleichen der Funktionalität der Sonnenuhr mit der anderer Uhren
– Schlüsse ziehen

 

So begriffen sie, dass die Sonnenuhr zum Zeit zeigen ungeeignet war.Also beschlossen wir, die Zeit doch mit modernen Uhren zu messen.

Viertens: Uhr bauen

Wie funktioniert eine Uhr?

Das ist eine Frage, die sich einige Kinder gestellt haben. Wenn man einen alten Wecker öffnet, sieht man sehr viele Metallräder und Achsen, beim Schütteln bewegen sie sich. Sie sind aber so klein, viel zu fein für die Kinderhände.

Aus einem Versandkatalog bestellte ich einen Uhr-Bausatz. Die Teile waren aus Kunststoff, groß genug, und ich versprach mir, meinem „Tüftler“ viel Freude damit machen zu können.

An einem Nachmittag war es so weit. Er packte die Einzelteile aus, überprüfte, ob alle da sind. Er schaute sie sich genau an, dann breitete er die Bauanleitung aus. Systematisch und geduldig legte er die Räder in die Fassung, Schritt für Schritt. Dann schloss er das Gehäuse, drehte an der Feder und wartete. Die Uhr ging ein paar Sekunden und blieb stehen. Also baute er sie noch mal auseinander und studierte noch genauer die Anleitung. Voll Zuversicht startete er noch mal, leider mit dem gleichen Ergebnis. Auch ich habe die Uhr zusammengesetzt, sie funktionierte nicht richtig. Er nahm sie mit nach Hause und wollte seinen Opa um Hilfe bitten.

Was aber positiv bei diesem Versuch war: Der Junge konnte sich ganz genau vorstellen, wie die Zahnräder ineinander greifen werden, wie sie die Zeiger treiben und wozu das Pendel dient. Er zeigte sehr viel Geduld, wollte selber das Problem lösen, überprüfte seine Vorgehensweise mehrmals und wusste, wo er sich Hilfe holen kann.

Wo sind die mathematischen Inhalte beim Bauen einer Uhr? würden sich Einige fragen. Die Zahlen auf dem Zifferblatt, die Zähne der Zahnräder, verschiedene Drehgeschwindigkeiten der Räder, das sind Inhalte, die Jeder als mathematische Inhalte erkennen würde. Aber es gibt noch mehr Mathematik in diesem Angebot.

Mathematische Inhalte:

  • Zuordnen der Teile zu den Abbildungen
  • Vergleichen der Zahl der Zähne, der Größe der Räder
  • Verständnis einer Anleitung und Einsicht in die Notwendigkeit der richtigen Reihenfolge
  • Verschiedene Geschwindigkeiten unterschiedlicher Räder

Die hoch begabten Kinder sind in der Lage, eine Bauanleitung richtig zu lesen, sie zu verfolgen und so zum Ergebnis zu kommen. Sie lassen sich durch die Misserfolge nicht entmutigen, sondern forschen nach Ursachen, wiederholen ihre Versuche. Sie begreifen das Zusammenspiel der Zahnräder und erklären den anderen Kindern, wie die Uhr funktioniert.

Hochbegabtenförderung:

– Lesen der Anleitung

– Organisieren der Arbeit

– Kontrolle

– Erklären der Funktion

– Begreifen der mechanischen Prozesse – wieso bewegen sich die Zeiger?

Fünftens: Kunst-Projekt

Eines Tages brachte ich meine Uhrensammlung mit in den Kindergarten. Ich legte sie auf ein Tuch, dazu hörten wir die CD mit „Time“ von Pink Floyd. An der Wand hing eine Abbildung des berühmten Bildes von Salvador Dali mit den hängenden Uhren.

Ich ließ den Kindern Zeit, um alles wahrzunehmen. Sie nahmen die Uhren in die Hände, hielten sie ans Ohr, drehten an den Rädchen, verglichen.

Das „Philosophische Gespräch“ mit den Kindern möchte ich Ihnen in Kürze darstellen:

„Wie fühlen sich die Uhren an?“
“Fest, kalt, hart.“

„Fühlt sich die Zeit auch hart an?“
“Die Zeit ist nicht hart, sie ist weich.“

„Kann man die Zeit in die Hand nehmen?“
“Nee…“ alle mussten lachen, ein Junge machte Kreisbewegungen und sagte: „Die Zeit läuft immer so.“

„Stimmt, es gab einen Maler, der das Gleiche gedacht hat, die Zeit kann man nicht halten, weil sie ständig weiter läuft und er hat es auf seinem Bild gemalt.“

So betrachteten die Kinder das Bild.

„Was ist auf diesem Bild hart?“
“Die Berge, der Tisch, der Baum…. Nein, der Baum ist nicht hart, er sieht tot aus, aber wenn die Uhr weiter tickt, dann kommt der Frühling, und der Baum lebt.“

„Und was ist auf dem Bild weich?!“
„Die Uhren, sie zeigen die Zeit, und die Zeit ist nicht tot, sie geht immer weiter.“

Die Natur der Zeit haben die Kinder wirklich verstanden, sie unterschieden auch zwischen der Zeit und dem Messgerät Uhr, was am Anfang des Projektes gar nicht so klar war.

 

Wir beschlossen, das Bild von Salvador Dali nachzumachen.

Bei diesem Projekt konnten sich alle Kinder aus der Gruppe beteiligen. Jeder brachte sein Können und Wissen ein. Bei einigen Kindern war es schon eine besondere Leistung, die Zahlen auf der Uhr lesen zu können und ihre Verwendung zum Zeitmessen zu begreifen. Die anderen konnten die Zahlen in der richtigen Reihenfolge ordnen. Nebenbei erkannten sie, dass sich der Weg der Zeiger auf der Uhr ständig wiederholt, dass nach zwei Runden ein neuer Tag beginnt und dass es damit kein Ende hat, weil auch die Zeit weiter läuft und kein Ende hat. Genauso wie ein Kreis keinen Anfang und kein Ende hat.

Alle Kinder machten unterschiedliche Sinneserfahrungen. Sie fühlten, wie hart die Oberfläche einer Uhr ist, wie weich die Modelliermasse ist, sie hörten Musik, betrachteten das Bild von Salvador Dali, mischten Farben beim Malen, benutzten verschiedene Materialien zum Gestalten.

Die hoch begabten Kinder erkannten durch diese Sinneserfahrungen den Sinn der Zeit – ihre „weiche“, sich ständig bewegende Natur. Sie erkannten, dass sich Manches in dieser Bewegung wiederholt, aber gleichzeitig auch verändert, dass der Baum immer wieder im Frühling neue Blätter bekommt, aber wenn viele Jahre vergangen sind, stirbt er. Genauso ist es mit den Menschen.

Das, was sich dagegen hart anfühlt, verändert sich nicht, lebt nicht, so wie die Uhren und die Berge. Ihre Zeit kann „unendlich“ werden.

Weil dieses Projekt so komplex war und einen großen Anklang bei den Kindern fand, kamen bei einigen bis jetzt unerkannte Begabungen zum Vorschein. Ein vierjähriger Junge zeigte, dass er die Zahlen lesen und ordnen konnte, ein anderer, der sonst immer vor den Angeboten flüchtete, benutzte seine Ellenbogen, um sich einen Platz beim Gestalten zu erkämpfen. Ich staunte über seine hohe Motivation und Ausdauer.

Mathematische Inhalte:

  • Wahrnehmen der Vergänglichkeit der Zeit
  • Wahrnehmung der Veränderungen in der Zeit
  • Tempo der Veränderungen: schnell, langsam, „keine“ Veränderung
  • Zuordnen der Geschwindigkeiten zu den Objekten: Uhr tickt schnell, Baum verändert sich im Jahres-Rhythmus, die Berge fast gar nicht
  • Kreis als eine adäquate Form zum Darstellen einer Uhr – die Zeiger bewegen sich im Kreis, unterschiedlich schnell
  • Aufbau einer Uhr
  • Zahlen
  • Bedeutung der Zahlen auf der Uhr
  • Gestalten/Formen der Zahlen
  • Richtige Reihenfolge der Zahlen auf der Uhr

Hochbegabtenförderung:

– Aktive Beteiligung an der Diskussion
– Erkennen der Zustände, Prozesse
– Entwickeln eigener Ideen
– Erklärungsversuche: Was war der Grundgedanke?
– Feinmotorische Tätigkeiten (Kneten)
– Beteiligung an gestalterischen Tätigkeiten
– Erklären, Bericht an die Zuschauer

Das fertige Bild bekam einen Sonderplatz im Raum und wurde den Eltern von den Künstlern erklärt.

 

Sechstens: Zähne putzen

Bei diesem Projekt beschäftigten wir uns mit Algorithmen. Der Begriff des Algorithmus ist ein zentraler Begriff der Mathematik.

Siehe auch: Grundideen der Mathematik .

Er bedeutet: eine Folge von Anweisungen (Schritten), die einen Prozess definieren, der mit gewissen Dateneingaben beginnt und nach endlicher Zeit ein eindeutig bestimmtes Resultat liefert.

Jede sinnvolle, gewollte Tätigkeit könnte man als einen Algorithmus darstellen.

Zum Beispiel „Zähne putzen“.

Eines Tages fragte ich einige Kinder: „Was muss man Alles tun, um die Zähne sauber zu bekommen?“ Ich bekam sehr viele Antworten, alles Mögliche durcheinander.

„Wie werdet ihr das einem erklären, der sich noch nie Zähne geputzt hat?“

Gemeinsam haben wir uns vorgestellt, wir wären im Waschraum und wollen Zähne putzen.

Also fingen wir mit dem Becher holen an. Den Becher füllen wir mit Wasser, spülen den Mund aus. Dann die Zahnpastatube aufmachen, eine kleine Menge Zahnpasta auf die Bürste rausdrücken, Zähne bürsten: oben, unten, Kauflächen hin und her, Seiten kreisend, ausspucken, den Mund spülen, den Becher und die Zahnbürste sauber machen, weg bringen, den Mund abtrocknen, fertig.

Mathematische Inhalte:

  • Algorithmen
  • Erkennen der Einzelschritte bei einer komplexen Tätigkeit
  • Richtige Reihenfolge führt zum Ergebnis
  • Alle Einzelschritte sind notwendig zum Erfolg

Hochbegabtenförderung:
– Durchdenken des Ablaufs einer komplexen Tätigkeit

– Erstellen einer Kette: Ursache-> Zustand-> Aktion->Auswirkung

– Überlegungen: „Was passiert, wenn ich ein Teil der Kette weg lasse?“

– Überlegungen: „Was passiert, wenn ich die Reihenfolge ändere?“

Algorithmen regeln den Ablauf und bringen uns sicher zum Ziel, wenn wir alle Schritte in der richtigen Reihenfolge machen. Auch mathematische Operationen sind Algorithmen. Einer der ersten ist, wie man eine Zahl schreiben muss, später: wie man addiert und andere Rechenarten vollzieht, welchen Weg man gehen muss, um eine unbekannte Zahl zu finden, eine Funktion zu bestimmen usw.

Den hoch begabten Kindern machte es viel Spaß, verschiedene Algorithmen zu bestimmen. Wir nannten es Rezepte.

Für das „Zähne putzen – Rezept“ machten wir eine Fotoreihe. Wir klebten die Bilder auf einen Streifen und hängten das Rezept im Waschraum auf.

 

Siebtens: Bohnen züchten

Zum Jahreswechsel singen Kinder sehr viele Lieder, aber eins ist besonders beliebt – es ist „Die Jahresuhr“:

„Januar, Februar, März, April – Die Jahresuhr steht niemals still – Mai, Juni, Juli, August – wecken uns allen die Lebenslust. September, Oktober, November, Dezember – und dann, und dann fängt Alles wieder von Vorne an!“ (Kann man wie einen Rap singen.)

So begreifen die Kinder, dass man die Zeit mit den Jahren messen kann, z. B. das menschliche Leben oder das Leben der Pflanzen. Das menschliche Leben dauert sehr lange, das wissen schon die Kinder, aber man kann versuchen, das Leben einer Bohnenpflanze zu messen.

So starteten wir ein Gärtnerprojekt. Die Kinder setzten die Bohnenkerne verschiedenen Bedingungen aus:

  • im Wasser/ ohne Wasser
  • in einer offenen Schale/ in der dunklen Filmdose
  • in der Erde/ ohne Erde
  • im offenen Behälter/ im geschlossenen Behälter

Die Bohnen wurden jeden Tag begutachtet, ein Kind dokumentierte die Veränderungen in einer Tabelle, und zum Schluss wurden die Bohnen mit einer Zahl fotografiert, die dem Experimenttag entsprach. So erlebten die Kinder, wie sich das Leben in der Zeit entwickelt und dann wieder verkümmert.

Als die Bohnen geerntet wurden, haben einige Kinder grafisch dargestellt, wie viele „Kinder–Bohnen“ eine „Mutter–Bohne“ hat. Dafür untersuchte jedes Kind eine ganze Pflanze. Danach wagten wir vorauszusehen, wie viele „Enkel–Bohnen“ wir dann nächstes Jahr bekämen.

So lange haben wir nicht gewartet, wir erstellten ein Bilderbuch über einen Zwerg, der im Herbst seine Freunde zum Bohneneintopf einladen wollte. Wir haben auch selbst gekocht, so endete die Zeit der Bohne in unserem Bauch.

Bei diesem Projekt beobachteten die Kinder nicht nur das Wachstum der Bohnenpflanzen. Sie beobachteten auch das Wachstum der Zahlen.

Beim täglichen Dokumentieren legten sie die Zahl, die dem Versuchstag entsprach. Es fing mit „1“ an, am nächsten Tag war „2“ dran, am dritten „3“ und so weiter. Die Zahlen wuchsen immer um „1“. Bis zum Erntetag.

Es war besonders spannend, als die Zahl die Zehn überschritten hat – wie schreibt man „11“? Dann die nächste Hürde. Wie wird „21“ geschrieben? „1“ und „2“ oder „2“ und „1“? Manche Kinder wussten schon genau, wie die großen Zahlen geschrieben werden, die anderen lernten daraus und machten eigene Vorschläge. Sie verstanden, dass man die Zahl „umgekehrt“ schreibt.

Aber nach der Ernte erlebten die Kinder noch eine Art des Wachstums der Zahlen: die Potenz. Aus einer Bohne entstanden 15 „Kinder-Bohnen“. Wenn man sie alle nächstes Jahr in die Erde einpflanzen würde, dann hätte man 15 mal 15 „Enkel-Bohnen“ bekommen, und wenn man sie wieder alle züchten würde, dann hätten wir 15 mal 15 mal 15 „Urenkel–Bohnen“ bekommen. Die hoch begabten Kinder versuchten sich die Zahl vorzustellen. Ich habe ihnen vorgeschlagen, es aufzumalen. Es waren sehr viele neue Bohnen. Auf diese Weise konnte man nach ein paar Jahren zu einem wahren Reichtum kommen. Aber wer mag nur Bohnen essen?

Was macht man mit so vielen Bohnen? Man kann sie gegen etwas anderes tauschen, z. B. gegen Kartoffeln, oder Möhren. Man kann die Bohnen verkaufen und sich etwas zum Anziehen kaufen.

So begriffen die hoch begabten Kinder, wie Wirtschaft funktioniert. Genauso ist es mit dem Getreide: Der Bauer kann sein Korn, das er nicht aufbrauchen kann, verkaufen und sich für das Geld andere Sachen kaufen.

Mathematische Inhalte:

  • Wahrnehmung der Veränderungen in der Zeit/Wachstum /Sterben
  • Schreiben der Zahlen in wachsender Reihenfolge
  • Veränderung der Mengen
  • Zusammenrechnen (Bohnenkinder)
  • Potenz – Erkennen des Phänomens der „Vermehrung“
  • Tausch/ Handel/ Preis
  • Voraussehen der zukünftigen Ergebnisse aufgrund der Erfahrungen

Hochbegabtenförderung:
– Dokumentation des Versuches
– Ausfüllen von Beobachtungsblättern
– Verantwortung für den Ablauf des Versuches übernehmen
– Zählen größerer Mengen
– Addieren und Subtrahieren/ Darstellung
– Koordinierungstätigkeiten bei der Herstellung des Bilderbuches
– Nachvollziehen der Lebensmittelgewinnung durch einen gezielten Anbau
– Nachvollziehen des Handels als Tauschgeschäft
– Nachvollziehen von Wirtschaftsbeziehungen

Achtens: Zeit-Rolle

Die vielen Angebote und Gespräche über die Zeit brachten auch die Frage, wie lange geht die Zeit schon, wann hat sie angefangen? Da wusste Jan genau bescheid: mit dem Urknall. Vor Milliarden Jahren. Und wie lange ist das her?

Um es den Kindern zu verdeutlichen, habe ich eine etwa zwanzig Meter lange Papierbahn benutzt, die zu einer Rolle aufgerollt wurde.

In der Mitte der Rolle war auf dem Papier noch nichts, so wie am Anfang des Universums. Der feste Kern war dunkel, es war der Urknall. Dann bemalte ich die obere Seite der Rolle, ausgehend von Rot in der Mitte, über Orange, Gelb bis Grün. Unser Weltraumexperte konnte es wunderbar nachvollziehen und erklärte den anderen Kindern: Am Anfangs war Nichts, dann knallte es, es entstanden Sterne und Planeten, und es war Alles noch sehr heiß, dann hat es sich abgekühlt, und als es auf der Erde grün wurde, da waren es die Pflanzen und die Tiere. Und natürlich nicht solche wie heute, sondern Dinosaurier. Aber es ist schon lange her, und die sind ausgestorben.

Das wussten auch schon andere Kinder.

Also das andere Ende der Rolle, das ist Heute. Wenn man die Rolle abwickelt, geht man in der Zeit zurück, bis in die Dinosaurier-Zeit. Das haben wir auch getan, einige Kinder malten ein paar Dinos, andere schauten sich Bücher an über die Geschichte der Erde. Nach einigen Tagen bevölkerten schon mehrere Dinos die Zeit-Rolle.

Bei diesem Projekt waren es die hoch begabten Kinder, die den anderen die Zeit erklärt haben. Es war erstaunlich, wie viel Wissen sie zu diesem Thema schon hatten. Besonders Jan verstand, wie die Materie im Weltraum zum Leben erwachte. Er wusste, dass es Milliarden Jahre gedauert hat, bis sich die Erde abgekühlt hat, so dass die ersten Pflanzen und Tiere sie bevölkern konnten. Er konnte die Zeit noch auf eine andere Weise messen, nämlich mit den wichtigsten Ereignissen.

So weckte er auch bei den Anderen das Interesse an der Erdgeschichte.

Er suchte bei mir nach Bestätigung seines Wissens und die gab ich ihm. Ich brachte in die Gruppe Bücher mit, in denen man das Entstehen des Lebens betrachten konnte. Erst kurz vor dem Ende entdeckten die Kinder die ersten Menschen.

Zu dieser Zeit sah die Erde anders aus als heute, es gab keine Häuser, keine Straßen mit Autos, die Menschen trugen Kleider aus Fell. Sie lernten Feuer anzuzünden, aßen zum ersten Mal gegartes Fleisch. Wie viele Menschenleben hat es gedauert, bis man so lebt wie heute?

Plötzlich erkannten die Kinder, dass es sehr großen Zahlen gibt, sie konnten sie nicht benennen, aber durch das Betrachten der Geschichte haben sie ihr Ausmaß nachvollzogen. Sie wissen, dass die Zeit weiter läuft, keiner weiß wie lange noch, also die Zeit ist unendlich, wächst mit jeder Sekunde, Minute, mit jedem Jahr usw.

Die Zeit bewegt sich nur in eine Richtung, aber man kann an die Vergangenheit denken – man kann nicht die Dinosaurier jagen, aber man kann sie in der Zeit-Rolle malen.

Immer wieder holten sich Kinder die Rolle und malten darin. Wenn sie Dinosaurier und Urmenschen malen wollten, mussten sie sehr viel abwickeln. Für die erste Lokomotive nicht so viel, noch weniger für die Autos. Eine der neuesten Erfindungen der Menschen, das Handy, malt man am offenen Ende.

Mathematische Inhalte:

  • Unendlichkeit der Zeit
  • Vergangenheit, Gegenwart, Zukunft
  • Bewegung in der Zeit: vorwärts und rückwärts
  • Zeiteinheiten: Sekunde, Minute, Stunde, Tag, Monat, Jahr, Jahrzehnte, Ära
  • Tempo der Veränderungen – immer schneller
  • Menge der Veränderungen – immer mehr
  • Gespür für Relativität der Länge des Lebens

Hochbegabtenförderung:
– Einbringen von Wissen über das Phänomen Zeit
– Einbringen von Wissen über das Weltall
– Einbringen von Wissen über die Geschichte der Erde
– Verständnis für große Zahlen entwickeln
– Nachvollziehen von Veränderungen in der Zeit
– Nachvollziehen der Unumkehrbarkeit der Zeit
– Nachvollziehen der Gesetze der Natur

Dieses Projekt dauerte viele Monate.

Es brauchte seine Zeit, die Zeit zu begreifen. Und der einzige Weg war natürlich, viele Erlebnisse in einer Kette zu erleben.

Um das Vergehen der Zeit zu verstehen, kann man die Ereignisse dokumentieren und bei einer späteren Betrachtung sich daran erinnern.

Jedes Thema eignet sich, um die verschiedenen Begabungsarten der Kinder zu erkennen und zu fördern. Zu jedem Thema kann man verschiedene Angebote durchführen, die mehrere Bereiche der kindlichen Entwicklung ansprechen.

Das Ansprechen mehrerer Sinne stärkt die Aufmerksamkeit, verlängert die Konzentrationsdauer und erschafft eine besondere Atmosphäre, die die Motivation begünstigt.

Durch Einbeziehen von individuellen Begabungen und Stärken wird die Zugehörigkeit des Einzelnen zur Gruppe gestärkt. Die Gruppe profitiert von Begabungen der Einzelnen, bekommt Anreize und wird bei der Entwicklung stimuliert.

  • Mathematische Förderung steckt in allen Bereichen der Arbeit mit Kindergartenkindern.
  • Sie muss nicht die schulischen Inhalte vorziehen.
  • Sie fängt bei einfachsten Funktionen an, wie Ordnen, Sortieren, Pärchen suchen und ist nach oben offen. Die Fähigkeiten und Interessen der Kinder entscheiden, wie weit sie sich vorwagen wollen (Mengen erfassen, Zahlen lesen, Zahlen schreiben, rechnen).
  • Mathematische Förderung gelingt besonders gut, wenn alle Sinne angesprochen werden, auch Bewegung.

Eine besondere Ausbildung im mathematischen Bereich zum Fördern hoch begabter Vorschulkinder ist nicht notwendig, aber wichtig sind:

  • Aufmerksamkeit,
  • Gefühl für Rhythmus und Ordnung,
  • Spaß am Rechnen,
  • spielerischer Umgang mit Zahlen und mathematischen Operationen,
  • Kreativität,
  • Mut zum Neuen.
  • Austausch der Ideen unter Kolleginnen,
  • Betrachten der vorhandenen Spiele unter dem mathematischen Aspekt.
  • Positive Verstärkung der Kenntnisse und Interessen der Kinder,
  • Kleingruppenarbeit für die Kinder, die ähnliche Interessen und Fähigkeiten (Begabungen) haben.

Jeder Anlass im Kindergarten ermöglicht uns Erzieherinnen, Kinder in die faszinierende Welt der Mathematik zu führen.Es geht dabei um die Entwicklung des Verständnisses von Zahlen, Mengen, Operationen, Effekten und Phänomenen.

Wir dürfen es nicht vergessen, dass die Kinder, schon lange bevor sie in den Kindergarten kommen, etliche Erfahrungen auf mathematischem Gebiet gesammelt haben.
Es ist keine neue Welt, die man an die Kinder heranführt, deshalb sollten sie von uns mit Natürlichkeit und ohne Angst vor eigener Inkompetenz weiter begleitet werden. Es ist ja auch selbstverständlich, dass der Kindergarten kein Ort für das mühsame Üben vom „Zahlenschreiben“ ist. Dafür ist schon die Schule zuständig.

Alles andere kann sich zu einem wunderbaren Abenteuer entwickeln.

 

Copyright © Klaudia Kruszynski 2006, siehe Impressum .
Datum der Veröffentlichung 5.5.07

Basic Ideas of Mathematics

Posted on by

by Hanna Vock

 

Is mathematics more than dealing with numbers? Yes.

Do children have to be able to read and write numbers in order to begin their exploration of mathematics? No.

Is it possible to do more than learn counting in kindergarten? Yes.

And there is much more than counting going on anyway, even though hardly anybody is aware of it.

Dr. Dr. Gert Mittring, multiple world champion in mental arithmetic, computer scientist, pedagogue and psychologist from Bonn, directed my attention to a website, in which Prof. Winter from Aachen [Germany] had compiled the “Basic Ideas of Mathematics”. Ever since then these ideas have been a major point of focus in our IHVO-Certificate-Courses .

Mathematics is an eminently abstract science – many are intimidated by this, many gifted children, however, are fascinated by just that. Many gifted children are quite able to think in abstract rather than concrete terms and they love to discover the abstract correlations within the visible world.

 

…in a nutshell …

Even higher mathematics go back to a few basic ideas. Children at pre-school age learn a great deal about these basic ideas.

The task of promoting mathematics in kindergarten lies in the conversion of these basic ideas into playing concepts.

And it is important to track down and to intentionally utilize the implicit mathematical content of every-day games and activities in kindergarten.

Yet, even then gifted children will ask for more …

(See also the articles The Advancement of Mathematical Talent in Kindergarten and Playful Mathematics at Kindergarten and Further Math-Projects.)

As a first thing there is

1) Symmetry.

To recognize symmetry is important for doing mathematics.
There is mirror symmetry and rotational symmetry.

Basically (nature is not pedantic) a butterfly is mirror symmetric. Its hypothetical axis of symmetry runs from its head down the length of its body to the bottom.

At kindergarten we use the inkblot technique (as used in the “pictures” for Rorschach tests) to create mirror symmetric pictures.

We can just as well use actual mirrors of different sizes to create or detect (possibly hidden) mirror symmetries in pictures. The children experience that, even though you can create a symmetric counterpart to any given picture, very few pictures dispose of their own implicit axes of mirror symmetry.

Now, there will be children who are not exactly thrilled by this – mathematically talented children, however, will be electrified. Some of them will experiment and search for ever new examples of mirror symmetries with remarkable endurance, others will be content to have discovered and understood the principle of mirror symmetry.

Many will long have been familiar with the phenomenon, some are even able to explain what it is all about.

The child is experiencing me, the kindergarten teacher, as somebody with similar interests when I discuss such mathematical phenomena with the child – I am seen as an interesting partner of conversation by the mathematically interested child, which is the best basis for further encouragement: as soon as we have entered into an expert dialogue the child can trust me with its questions and ideas and I can follow the child’s lead.

See also Communication in the Kindergarten.

Rotational symmetry in all its marvel is visible in mandalas. Rotational symmetry is a generating principle. By painting mandalas the children intuitively understand the inherent rotational symmetries.

So, does that mean it is possible to identify mathematically talented children by their fondness of painting mandalas? Not at all – unless you catch the narrow time span between two points: The point in time, when the child is intellectually ready to grasp the principle at all, and the point in time, when its understanding of the matter reaches certainty and firmness. This time span will, as matter of course, be rather short if a child is talented or even gifted in the mathematical area.

And once I’ve got it – why should I stick around? After all I’m here to learn new things.

So even though there is plenty mathematics in mandalas the simple colouring of a mandala is hardly ever satisfying for a gifted child. Beware, though, that oftentimes the principle of symmetry itself will be taken as much more interesting than the artistry in actually painting the mandala.

Children are discovering and seriously experimenting with symmetries when they suddenly begin building symmetric objects or when they string beads onto a thread. This is where mirror and rotational symmetry can be combined:

 

If a gifted child has created large symmetric buildings with coloured building bricks at the age of 2 – and has thereby worked out the problem of mirror symmetry – a pronounced interest in stringing beads is not likely to occur at the age of 4 or 5, if it does, it will be ephemeral, unless the thrill of it is in the shared activity and the chatting with other children who are stringing beads. But symmetry is not a new discovery then (consequently we cannot make an imagined ‘tick’ for ‘cognitive advancement’).

Children also experience mirror symmetry when perceiving their own bodies as consisting of two equal but mirror inverted parts. Many rhythmic moves and dances are symmetric. Symmetry is one major principle of construction in the world, especially in living beings, and hence is a basic idea of mathematics. And finally, it is also an aesthetic concept.

In physics as well symmetry is a basic principle. Physicists when discovering a particle or a force will immediately look out for the anti-particle or the counter-force, respectively.

One way of helping children appreciate symmetry is, for example, creating a symmetry book: taking photographs of symmetric things, then drawing the axes of symmetry onto the photographs and sticking them into a (paper-) notebook or onto a big poster. We play “symmetry detectives” with the children for a while.

There are many more possibilities …

Once again it’s up to you and your creativity …

There is a very nice piece of gaming material about this, see: ONLY A BOOK !!!

Interesting Games: „Spiegeln mit dem Spiegelbuch“ (Mirroring with the Mirror Book)

2) The Notion of Numbers and Their Positional Notation

No, being able to write numbers is not so important at first.

Even without this motor skill many children are fondling around with numbers in their minds, they meditate on numbers, sets and mathematical structures.

Recommended Reading: Mittring, Gert: What’s Happening Inside When We Do Arithmetic?

Writing numbers and the corresponding motor skills should not be an impediment to mathematical activities with the children. (We do not need letters for speaking either.)

If children want to write numbers, they will practice them tenaciously, as long as we provide the appropriate materials: a number panel, numbers made of cardboard, wood, foam rubber, a number puzzle, magnetic numbers, number stamps – which of these we offer does not make much of a difference, sometimes less can be more here. Younger children will however prefer numbers that are not only printed or drawn but numbers that come as little physical objects so they can experience them haptically.

Children acquire the notion of numbers early on and independently of the ability to read and write numbers, they understand that each number-word signifies a specific amount of things.

Beware: this is not the same as being able to say number-words in the correct order by heart. In order to really count one must have understood the correlation of a given number and the idea of a set of so many individual objects as signified by that number and this ability is eventually a rhythmic one (!). Very young children will oftentimes quickly lose their rhythm when counting objects, piece by piece, so that they lose track and the correct outcome becomes a matter of chance at best.

The notion of numbers also includes the ability to see beyond the ducks, teddy bears or candies and apprehend the quantity signified by the number. There are many pre-school exercise books on this topic … , however, many gifted children enter kindergarten with an operational understanding of numbers already. If they, for example, are able to convert the number on the tossed dice into the correct number of moves in a board game, it is obvious that they dispose of an abstract notion of numbers.

So then what is interesting for these children during their long time spent in kindergarten?

First of all: ever increasing numbers. Quite a few children quickly learn to count further and they are interested in the structure of the system of numbers (configuration in the decimal system) and they contemplate on this.

Do we want to leave them alone with this or do we want to accompany them in the venture as their partners?

Some children at pre-school age enjoy (and all the while learn a lot) counting in steps of 2, 3, 4, 5 and so forth. They try to count backwards, they ponder the relatedness of numbers, for example the relation ‘smaller – bigger’ or ‘even – odd’ (only even numbers can be divided by 2), they break numbers down into smaller numbers, in other words: they begin doing arithmetic.

Some children will make use of aids (stones or whatever), others perform theses mental operations in their minds only, abstractly.

Our number system (which most people in the world use) is based on the number 10 (decimal system). This is most probably due to the fact that we have 10 fingers. Basically we keep counting to 10 over and over again while we simply raise the digit in front by one every time we have counted to 10.

Some time in pre-school life the mathematically talented child discovers something else (or at least develops an intuition of it): When in the course of counting the first digit goes beyond 9 the entire number increases in length by one digit (from 9 to 10, from 99 to 100, from 999 to 1000). This is how the child closes in on the question of ‘place values’.

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

usw.

91

92

93

94

95

96

97

98

99

100

101

102

103

104

usw.

111

112

113

114

usw.

The insight is near: It is important to understand the place value of each digit in larger numbers. The 3 in 432 stands for 30 while the 4 signifies 400.

That is pretty much it.

It is not surprising, that mathematically gifted (pre-school) children will soon turn to more difficult considerations, for example: What is it with the points in numbers? What does 17.8 degrees really mean? What is 3.98 Euros? What is -7? What is an eighth? How does multiplication work?

See also the example of Lena in the article: Giftedness A Definition

Is there a colleague in the team who enjoys playing with numbers – is that possibly you?

Very well, then do play with numbers in kindergarten and involve those children who are interested.

3) Assignment and Function

In kindergarten there are all kinds of games in which entities have to be assigned to one another and at a certain developmental stage of their cognition children are constantly assigning things to other things: this is mine (not in the sense of ownership, but in the sense that ‘this thing and I belong together’), this is yours (correspondingly), that is Sven’s jacket, this is Lina’s hat…, they practise the mathematical operation of assignment, and it is fun to them.

So, whenever we offer or observe games being played in which things are to be assigned, games of whatever kind, the children are putting their knowledge into order, all the while building a basic mathematical understanding on the side. Many popular tabletop games are also based on the ability to assign objects correctly to another (and they are an exercise of this operation).

All this appears simple and easy to us; however, children have yet to develop these mental structures in their first years of life.

Gifted children will often do so at a very early stage. For example, there was a girl of one year and nine months, who had finished her own and now wanted her grandmother’s chocolate Santa, too. She was caught speaking to herself: “Naah, that’s grammy’s dollyman.”

Another girl, exact same age, uttered: “That’s Anna’s hammer, no, it’s Anna’s mother’s hammer.“

Assignment is a prerequisite for understanding mathematical functions. These are the often overwhelming terms, loaded with many x’s and y’s and latin or greek letters alongside many additional mathematical symbols, which will remain unintelligible to us non-mathematicians.

But there are simple functions as well, which children meditate and work out for themselves even as early as in their pre-school years, without any knowledge of their mathematical notation.

The Wikipedia definition of the mathematical term ‘function’ reads:

A function assigns exactly one value to each input of a specified type. The argument(input) and the (assigned)value may be real numbers, but they can also be elements from any given sets : the domain and the codomain(range) of the function.

At first sight this may look awfully complicated to us laymen (and indeed, anyone will receive undivided support on any TV talk show in Germany by declaring categorically: “No, mathematics has never been for me!”)

No doubt, there are extremely intricate mathematical functions which 99.99% of all people would lose their minds over – but luckily we are dealing with elementary education, we are talking about important basic knowledge .

Every function is basically an equation. This means you can do things on both sides of the equal sign, you might, for example, add something, but you must do it on both sides so that the equal sign isn’t lying.

Letters are used in equations to represent certain things or to signify values that are yet to be computed.

Implementing the above (Wikipedia) definition of a function the popular kindergarten game “Shoes on a Pile!” would be described mathematically:

There are 25 children in our group – they are all participating in the game. In the language of mathematics they are the elements of the set we are presently looking at, the so-called domain (“x-value”).

Now exactly one pair of shoes (the right pair, of course) is to be assigned to every child, to every element , that is. The 25 pairs of shoes are the elements of the range (“y-value ”) . Both sets have the same number of elements – 25 children own 25 pairs of shoes. Therefore there is exactly one corresponding “partner” for each element of both sets, a one-to-one mapping is possible and this gives us the simplest equation for a function there is:

y = x.

If we suppose every child had 2 pairs of shoes stored at kindergarten, we would have to assign 2 pairs of shoes (elements of the range) to each child (element of the domain) – no doubt, a somewhat more difficult task. The equation would then read: y = 2x (spoken: “y equals two x”). In spoken language this means: “How many pairs of shoes (y) are there if all children (x) each have two of them?” With 25 children this would amount to 50. We would not have enough space for so many shoes in our kindergarten, but some of our children would probably still be able to match each pair correctly with the right owner.

The advantage of such equations with x and y is that they allow for universally valid solutions to a given problem of assignment: “y = 2x” therefore does not only work for 25 children but also for 27 children, even if we wanted to determine the sum total of the children’s ears.

By the way, many a mathematically gifted and predisposed child will be rather irritated if even one child has thrown two pairs instead of the requested one pair of shoes on the pile. That ruins the function (this is a breach of the exact correspondence of one element from the domain with no more than one element from the codomain), and all the beauty, which the gifted child experiences in any kind of order, is spoiled.

Such functions are evident all over kindergarten. Every child has its little icon by its coat hook, every child has its own little locker, and so forth.

If we – just for the thrill of it and for mathematics’ sake – were to ask how many elements we came up with if we allowed the following categories of possessions owned by the children (every child has exactly):

1 last name (B), 2 first names (C), 1 icon at the coat hook (D), 1 coat (E) and 2 gloves (F),

Then the equation representing our function would read:

y = 1x B + 2x C + 1x D + 1x E + 2x F = 7x = 175

(with “ y “ being the sum total of possessions)

As we know that there are 25 children in the group, x=25 (children), this equation renders a value of y=175 possessions.

If three gloves were lost and five children complain because they only have one first name, we have to alter the equation:

y = 1x B + 2x C – 5 + 1x D + 1x E + 2x F – 3 summed up we get:

y = 7x – 8 = 175 – 8 and that comes to:

y = 167 (possessions).

So, what is this all good for? I don’t need “x” to figure this out!

Yeees, sure, but the point is that these obvious correlations in our everyday life represent just what is called a function in mathematics, and this is just to show how these ordinary facts of life can very well be translated into mathematical notation, in other words they are in and of themselves mathematical by nature, even if most of the time we don’t think of them as arranged in mathematically representable order. And children’s thinking cannot help following mathematically valid principles.

Carolin, 4 years of age, was working on the function y = a + b + c when counting cars. The sum total of cars driving by the house was the sum of ‘a’ (number of red cars), ‘b’ (number of white cars) and ‘c’ (number of all other cars).

She did so by first assigning every red car to one box on her sheet of paper, each white car to another box and all ‘other cars’ to a third box. Next she counted the cars of each of the subsets and finally added these numbers up.

You can find a detailed account of this episode in the article Custom-fit Cognitive Advancement.

An exciting application of ‘assignment‘ is inventing and using a cipher . In a simple version this can be done by assigning a certain symbol to every letter in the alphabet. This could be another letter – or a number or a little icon…

Highly gifted children, once they have tried this for a little while, often come up with complicated ciphers: The symbol to represent the original letter is determined by a specific general rule, as for example: A becomes D, B becomes E, C becomes F … (rule: replacement by third successor in the alphabet). One day, a gifted girl, five years old, was thrilled and delighted when discovering that she didn’t need a rule at all and could just as well write the lower row entirely at random, as, for example, like this:

A   B   C   D   E    F   G   H    I   J   K   L   M   N   O   P   Q   R   S   T   U   V   W   X   Y   Z
G  N   W   I   M   F   A    R   L   V   C  Q   U   H   Z    B   K   S    Y   O  X   T    P    D   E   J
„I’ll have to watch my table, though!”,

she said. What really tickled her was that she had set the F for the F. A truly clever idea for a five-year-old!

Some gifted children will even conceive of much more sophisticated systems. One six years old boy in kindergarten once let me in on the cipher he had just made up:

In a first step every letter is transformed into a number: A is 1, B is 2 …
Now all these numbers are raised to the power of 2, i.e. multiplied by themselves.

His name, Thomas, would then read: 400 – 64 – 225 – 169 – 1 – 361.

However, he still was not quite happy with the system:

“All it takes is someone to notice they’re all square numbers, then he knows that the 1 is the A, and the A is everywhere.”

He thought it would be safer to substitute the smaller numbers by prime numbers. Prime numbers are numbers that divide only by 1 and by themselves. He set the 37 for A, the 83 for B, the 131 for the C and the 137 for the very frequent E. With this, he reckoned, he had done enough to conceal the principle behind his cipher.

4) Part-Whole Relation

Three-year-olds and younger children often do not yet understand what is meant when somebody calls: “All children come here!”. Either they don’t react at all or, if they already have a notion of the word “all”, they may ask “Me too?” They are not aware that “all children” includes every single child, they still aren’t sure about the ‘part-whole-relation’. This is another example of a pattern of thought which every child has to develop and that has a lot to do with mathematics.

In order to understand the more advanced ideas of set theory or geometry this basic knowledge must be developed.

Even the easiest addition, as in 3 + 4 = ?, can only be performed on the basis of an understanding that objects, planes, sets can be divided into single parts and reassembled into a whole.

A child working on a puzzle is dealing with the part-whole relation, just like a child building a tower or taking apart an old alarm clock. Children discover that there are things which are made of parts that are the same (for example pieces of a pie – the whole is only a “more” of the same) while other things are composed of quite different parts which still add up to a whole, which is then of an entirely new quality (alarm clock).

Complex analytical and synthetisizing thought in mathematics has its origins in these early discoveries in childhood.

5) Algorithms

There is no need to fear this Arabic word.

An algorithm is a finite list of well-defined instructions by which to solve a given problem.

Recipes are algorithms. The interesting thing is, that it is not easy to say of how many steps an algorithm must be composed. In everyday life, for example in the case of recipes, much is assumed: The recipe neither says that the pot has to be put on the stove nor that the stove has to be turned on or that one has to watch when the food is hot and the stove has to be turned down – all the recipe says is: “heat up”.

This is one of the basic problems in recipes, manuals and pedagogics: How much can be assumed, how much must be explained?

Do I have to say, that the plug has to be stuck into the socket in order to operate an electric device? Or can I presume it? Or does the unexperienced cook, when told “heat up” possibly wonder: “Well, how? In a pan, in a pot, in the oven, and how do I know when it’s hot enough?”

Children have this problem all the time: “Wipe the table clean!” But what, if the child does not know the algorithm “wiping the table clean”? It has no concept and may sluggishly wipe across the table with its sleeve, while our idea (algorithm) was quite different: get a cloth (where?), wet the cloth (where and how?) and squeeze it (sufficiently), clear the table of all objects (where to put them?), wipe the table entirely (not all that easy to do) and wipe it dry (again the entire table top), put the cloth away (where?).

It’s not a bad thing to begin developing the routine “how to wipe the table so that it is clean afterwards” at the age of 3. It may come in handy when at the age of 11 one wants to do some cooking and not have the parents prohibit any further attempt because one has left the kitchen in a mess.

There are few 11-year-olds who enjoy learning how to wipe a table clean. 2-3-year-olds will love to do so with ardent zeal.

The more a person knows, the shorter an algorithm will do. It’s the same with computer programs. “If the computer “knows” a lot of helpful programs, if it disposes of an operating system and a number of subroutines, a word processing program can build on it. Mathematical algorithms, too, can be just the shorter the more mathematics the calculator (be it man or machine) understands already.

In order to act autonomously (in whatever area) the child must first build and “hard-wire” many, many basic algorithms in its brain, which it can then compile to more complex operations (“I’ll set the table, and I’ll wipe it clean first!”).

Having skills and abilities is just that: disposing of such algorithms (well-defined procedures). The actual acting out of such procedures reinforces the algorithm itself. Mistakes, misleads and detours are being eliminated (just like the so-called ‘Banana Softwares’ for computers, which got the name because, like bananas, they mature when already in the hands of the user). Then again, once clean of all bugs, an algorithm will guarantee a quick success, oftentimes to become increasingly mechanized; that frees the mind for new strategies and creative ideas.

Unfortunately in many families there is way too little being done with respect to such cognitive developmental processes. As a result there are children who lack all independence and who “don’t really know” how to do anything. On the other hand there are well fostered adepts, who seem to be managing things at ease, who make their own sandwiches or plant a flower at the age of three, who know how to cross a street safely, how to settle a dispute or how to agree on the rules of a game when they are five years of age.

Deliberate action is best learned by acting deliberately. This is where kindergarten is at an advantage: The children are requested to be self-reliant, self-reliance is valued highly, the children learn, for example, to do handicraft works with more and more deliberation and consideration for the limitations set by the current situation…, the more children are encouraged to act upon good thought and planning, which includes readjusting strategies and checking results, the better.

By making it a point to habitually reflect and evaluate each step in a work process together with the children, when they are not yet entirely familiar with it, we make them aware of the underlying algorithms and promote their autonomy as well as their basic understanding of mathematics. Children who are being involved in the household chores, at home too , in gardening and DIY activities around the house or any other result-oriented tasks as early as possible are clearly at an advantage. They also lay the necessary groundwork for a later ability to conceive of capable algorithms like “how to plan our wedding” – or by the same token to design computer programs, create recipes or write manuals (further important skills and talents presumed).

6) Measuring

What are all the things that can be measured? And how is it done? And why measure things at all?

IHVO course participants who worked on the topic of measurement with kindergarten children were thrilled to see how intensely, intelligently and persistently these children occupied themselves with these questions.

Starting with the simple measurement of length, width and depth (for young children this is, of course, new), going on to measuring weight, temperature, time and volume. Their activities ranged from making measurements to creating technical constructions on to considering philosophical questions (What is time? What is infinity?), then even raising health concerns (regularly check the temperature inside the refrigerator, take everybody’s temperature before they are allowed to enter kindergarten).

Here too, it is a good method to get as many children as possible acquainted with the simple principles of measurement and then to observe: Which children want / need more input? However, it is not necessarily a good idea to start with all children and take it siiiiiimply and sloooowly and trust that the brighter and more curious ones will await the slower ones’ catching on, and that the brighter ones will still want to continue. Oftentimes they will turn away either inwardly or outwardly.

Starting with the children, who are not so strong (in this area), and watching how far they are interested and willing to go with this, taking all the necessary time even for the simple aspects has proven to be the better idea. One can take those children aside, who are stronger (in this area), the ones that are more talented, capable, knowledgeable and motivated, and go about the issue separately with them, rush through or even skip the easy stuff and go straight to the more involved questions. For example: How can we measure which of two stones of similar size is really the bigger one? What exactly does “bigger” mean: taller, wider, greater mass or volume? (Hint: check the displacement of water.) And which one is heavier? (If we compare both, volume and weight, this will lead to the question of density.)

An understanding of measurements and methods of measuring broadens the horizon with regard to mathematical questions and scientific research.

Acquiring instruments of measurement and familiarizing children with them, always keeping them in reach for the children, has proved its worth. Ruler, measuring tape, folding rule, measuring cup, thermometer (without mercury), different clocks including self-made clocks (sundial, water meter), different kinds of scales (kitchen scales, letter scales, traditional scales with two pans and balance weights).

All this fascinates children.

See also: Number Detectives Are Taking Measurements.

7) Approximation, Estimates

At summer festivals there are sometimes these interesting guessing games: How many peas or marbles are there in this jug? Whoever comes closest with his estimate wins the prize. Often it is not until then that we realize how poor our ability to give an estimate really is. Many people do not really know what they are being told, when someone gives them directions: “It’s about 800 meters to the station.”

Anything, that can be counted or measured, can also be estimated: number of, weight, speed, wind force, temperature, length and distance, height and depth, brightness, loudness, solidity of materials, time span, shape (this is just about spherical)…

What does this have to do with mathematics, and why should children learn it?

It makes sense to acquire a sense of speed, of amounts and other things as early as possible. It makes for a sense of orientation in the world and gives a person security when acting. If I knew that the person giving me directions (800 meters to the station) knew the area and was able to give a safe estimate, and if, in addition, I knew how many meters I cover per minute when walking, I could easily assess whether I can take my good old time or whether I better hurry up to make it in time for my train.

It is also rather helpful to be able to estimate the bill at the restaurant in order to detect possible errors on the bill right away. Being able to judge orders of magnitudes is often important and helpful in everyday life. Scientific mathematics, economic mathematics and statistics make use of estimates, too, which often saves time and money while still rendering sufficiently precise results.

******************************************************

Some more things that interest gifted pre-school children early on:

Maps (also city maps, blue-prints …):

Just about anything that is an abstract representation of the real world and thereby helps to orient oneself in reality. Of course, creating and drawing maps and sketches is also highly interesting and instructive for gifted children.

More about this: Plans, Drawings, Sketches, Mind-Maps.

Pondering Probabilty and Chance.

The concept of „random chance“ is hard to grasp for many young children. Have they not just spent considerable mental effort in understanding that there is always a cause for everything, and that all events taking place in the world are composed of cause and effect. Consequently they will at first tend to hold someone “responsible” even when an event was purely accidental. Eventually their intellectual development will enter the next level and they will come to see that some things happen by chance, which also means that these things are hard to foresee and impossible to control. Random events can only be awaited. See also: Examples of Great Interest in Systems and Logical Relations. (The example of Daniel and the Christmas Calendar, publicized October 30 th , 2008). But children of high intelligence are never satisfied with what they have understood, they are quick to conquer new concepts and constructs, preferably the concept of probability comes next. Even the advent of a random occurrence can be estimated and calculated.

By attaining an ever deepening understanding of this concept, the child will develop the program “risk assessment”, which is being refined over time and will eventually become a routine running in the background at all times.


If a child reaches this intellectual state very early on, say at an age of 3 or 4 years, it may happen that this child will be considered extraordinarily fearful. More details on this in Timidity and Apprehension in Gifted Children.

The Number Zero.

The number zero is still young. The peoples of India, Babylon, China, Greece and other peoples developed sophisticated numeric systems and mathematics as far back as several thousand years ago. Yet, the number zero was only conceived of some 500 years into our common era. No earlier than in the 11 th century was it introduced in Europe.

What is so difficult about the zero can hardly be observed with gifted pre-school children: They deal with it at ease. Only when it comes to dividing by zero, the issue becomes mysterious, because dividing by zero is “not possible”. There is never a definite result, it always comes to “infinite”.

Hint:

At the Museum „Arithmeum“ in Bonn (offering good guided tours for children, even for kindergarten children if they have an interest in numbers and calculating) much can be learned about the history and the techniques of calculation.

http://www.arithmeum.uni-bonn.de/

Picture Books / Special Interest Books on Numbers and Mathematics.

Zahlenmärchen

(Fairy Tale of Numbers)

By Ida Fleiß and Gert Mittring. Wagner Publishing.

[Note by the translator: The English titles in brackets are merely translations, they do not represent actual titles of English Publications of the books, which to our knowledge there are none.]

Today there are quite a few picture books dealing with the numbers ranging from 1 to 10, which gifted children often tackle as early as in their 2 nd or 3 rd year of life. This book even goes beyond and is therefore interesting for the math-aficionados among the elder kindergarten children, too.

It is a fairy tale taking place in Numberland. Gert, the world-champion of mental arithmetic, takes them on an interesting tour. They visit the Number-Clinic, the Symbol-Factory, the café with its digit-coffee and root-cake, they go to Niners-City and check the Number-Museum, finally they reach the Cave of Numbers.

On their trip by train they listen to suspenseful fairy tales:

* The Number Spider
* How the Three Found True Friends
* A Dino in Love
* The Tale of King Divisibility II
* The Secret of the Dancing 8
* The Dreamdealer
* The Devil and the Number-Witch
* The Tale of the Smart 5

… and it’s always about numbers.

Each fairy tale as well as each stop on the journey can be read out of sequence, so that the children may discover the contents of the book step by step.

A book for kindergarten and elementary school children who consider numbers their friends and enjoy dealing with them.

Das Bilderbuch von Zahlen

(The Picture Book of Numbers)

by Rolf and Margret Rettich, Ravensburger Publishing House
This is a picture book on numbers ranging 1 to 10, maybe the book of choice for very young gifted pre-school children.

Kindergartenspaß mit Willi Wiesel. Zählen und Tüfteln.

(Fun at the Kindergarten with Willi Wiesel. Counting and Puzzling.)

Ensslin Publishing.
A workbook for counting and colouring. Also covers only the numbers from 1 to 10, so don’t offer it too late!

Komm mit ins Zahlenland. Eine spielerische Entdeckungsreise in die Welt der Mathematik

(Come Along to Numberland. A Playful Quest into the World of Mathematics)

by Gerhard Friedrich and Viola de Galgóczy.
A didactic book of games and stories on the numbers 1 to 10. Appropriate for kindergarten. Interesting for gifted children between ages 2 and 4, while they are in the process of discovering the numbers up to 10, not so thrilling once that number range has been mastered.

Was ist Was, Band 12: Mathematik

(What’s What, Vol. 12: Mathematics)

Tessloff Publishing
The book comprises many good illustrations and explanations, good reference reading for teachers as well.

 

The translation of this article was made possible by
Jordis Overödder, Kürten, Germany.

Copyright © Hanna Vock 2007, see Imprint.
Translation: Arno Zucknick
Date of publication in German: September 4 th , 2007

Grundideen der Mathematik

Posted on by

 

von Hanna Vock

 

Ist Mathematik mehr als der Umgang mit Zahlen? Ja. Müssen Kinder zuerst Zahlen lesen und schreiben können, um dann mit Mathematik beginnen zu können? Nein. Kann im Kindergarten mehr passieren als Zählen lernen? Ja.

Und es passiert auch ganz viel mehr, auch wenn es den Beteiligten oft nicht bewusst ist.

Dr. Dr. Gert Mittring, mehrfacher Rechenweltmeister, Informatiker, Pädagoge und Psychologe aus Bonn, machte mich vor Jahren auf eine Zusammenstellung im Internet aufmerksam, in der Prof. Winter aus Aachen die „Grundideen der Mathematik“ zusammengestellt hatte. Seitdem werden diese Grundideen in den IHVO-Zertifikatskursen besprochen.

Mathematik ist eine besonders abstrakte Wissenschaft – das ist für Viele zum Fürchten, für viele hoch begabte Kinder liegt aber gerade darin die Faszination. Viele hoch begabte Kinder sind sehr früh zum Abstrahieren vom Konkreten fähig und lieben es, hinter (?) der konkreten Welt abstrakte Zusammenhänge zu entdecken.

(Siehe auch die Beiträge Mathematische Begabungsförderung im Kindergarten und Spielerische Mathematik im Kindergarten und Weitere Projekte zur Mathematik und Erzieherinnen unterstützen Kinder beim Rechnen lernen.)

… kurz gefasst …

Auch die höhere Mathematik basiert auf einigen Grundideen. Kinder im Vorschulalter lernen ganz viel über diese Grundideen.
Aufgabe für die mathematische Förderung im Kindergarten ist es, diese Grundideen in Spielideen zu verwandeln.
Und es ist wichtig, in den Spielen, die wir sowieso spielen, und in den Tätigkeiten, die im Kindergarten alltäglich sind, die mathematischen Inhalte aufzuspüren und bewusst zu nutzen.
Aber auch hier wollen die hoch begabten Kinder mehr…

Da haben wir zuerst die

1) Symmetrie.

Symmetrien zu erkennen ist wichtig, um Mathematik zu betreiben.

Es gibt die Klapp-Symmetrie und die Dreh-Symmetrie.

Im Prinzip (die Natur ist hier nicht pedantisch) ist ein Schmetterling klapp-symmetrisch. Die (gedachte) Klapp-Achse verläuft vom Kopf bis zum Hinterteil längs durch seinen Leib. Schön, dass er das „Klappen“ mit seinen Flügeln sogar immer schön vorführt!

Mit Klecksbildern stellen wir im Kindergarten klapp-symmetrische Bilder her.

Wir können aber auch mit einem Spiegel beliebiger Größe Klapp-Symmetrien herstellen oder auch die (eventuell vorhandene) Klapp-Achse bei Bildern suchen. Die Kinder machen dabei die Erfahrung, dass man zwar zu jedem Bild ein klapp-symmetrisches herstellen kann, dass aber beileibe nicht jedes Bild von sich aus eine Klapp-Achse hat.

Nun gibt es Kinder, die dies nicht interessiert oder gar vom Hocker wirft – mathematisch interessierte und besonders begabte aber schon. Manche von ihnen experimentieren und suchen dann mit erstaunlicher Ausdauer nach immer neuen Klapp-Symmetrien, anderen genügt es, das Prinzip, das Phänomen Klapp-Symmetrie erkannt und begriffen zu haben.

Viele haben es schon längst von selbst erfasst, manche können auch ausdrücken, worum es dabei geht.

Indem ich als Erzieherin mit dem Kind über diese mathematischen Phänomene spreche, wird klar, dass wir ähnliche Interessen haben – ich werde zum interessanten Gesprächspartner für das mathematisch begabte Kind, die beste Grundlage für Förderung: Sobald wir in einen „Fachdialog“ eingetreten sind, kann mir das Kind seine Fragen und Ideen anvertrauen, und ich kann mich davon leiten lassen.

Siehe auch: Kommunikation im Kindergarten.

Dreh-Symmetrie findet sich in wunderbarer Weise in Mandalas. Denn Dreh-Symmetrie ist ihr Erzeugungsprinzip. Indem Kinder Mandalas malen, erfassen sie die intuitiv die darin enthaltenen Dreh-Symmetrien. Sind jetzt mathematisch besonders begabte Kinder daran zu erkennen, dass sie gern Mandalas malen? Überhaupt nicht – es sei denn, man erwischt genau den schmalen Zeitraum zwischen zwei Zeitpunkten: Dem Zeitpunkt, an dem sie geistig so weit sind, dass sie das Prinzip erkennen können, und dem Zeitpunkt, in dem sie es sicher begriffen haben. Diese Zeitspanne ist auf Grund der besonderen und vielleicht sogar hohen mathematischen Begabung aber naturgemäß sehr kurz.

Und was ich sicher weiß – warum soll ich mich ausdauernd damit beschäftigen? Schließlich bin ich auf der Welt, um Neues zu lernen.

Obwohl in Mandalas also viel Mathematik steckt, ist das Ausmalen für hoch begabte Kinder selten spannend – eher könnte es sie interessieren, wie man selbst ein Mandala konstruieren kann. Aber Vorsicht, es interessiert dann oft weniger die künstlerische Ausführung als vielmehr das Symmetrie-Prinzip.

Kinder entdecken und experimentieren auch mit Symmetrien, wenn sie plötzlich symmetrische Bauwerke bauen oder wenn sie Perlen auffädeln. Hier kann man Klapp- und Drehsymmetrie toll kombinieren:

Wenn ein hoch begabtes Kind mit zwei Jahren umfangreiche symmetrische Bauwerke aus farbigen Bauklötzen erstellt hat – und sich damit das Problem der Klappsymmetrie erarbeitet hat, dann ist das Interesse am symmetrischen Perlenauffädeln mit vier oder fünf Jahren aber kaum noch zu erwarten, oder es ist nur flüchtig. Es sei denn das Kind findet es verlockend, mit anderen Kindern, die das Gleiche tun, zusammen zu sitzen und gemütlich zu schwatzen. Aber die Symmetrie ist dann keine neue Entdeckung für das Kind (d. h. wir können in unserem Kopf für dieses Kind kein Häkchen bei „kognitive Förderung“ machen).

Kinder erfahren Symmetrie auch am eigenen Körper, indem sie ihren Körper in zwei klapp-symmetrischen Hälften wahrnehmen. Viele rhythmische Bewegungen und Tänze sind symmetrisch. Symmetrie ist ein wesentliches Bauprinzip unserer Welt und vor allem auch der Lebewesen, und ebenso eine Grundidee der Mathematik. Und Symmetrie ist auch ein ästhetisches Prinzip..

Auch in der Physik ist Symmetrie ein Grundprinzip, zum Beispiel suchen Physiker, wenn sie ein neues subatomares Teilchen oder irgendeine Kraft entdecken, sofort nach dem Antiteilchen bzw. der Gegenkraft.

Eine Möglichkeit, Kindern Symmetrien bewusst zu machen, ist zum Beispiel, ein Symmetrie-Buch anzulegen: symmetrische Dinge fotografieren, auf dem Foto die Symmetrie-Achse(n) einzeichnen und das Ganze in ein Heft oder auf ein Poster kleben. Wir betätigen uns mit ein paar Kindern eine Zeitlang als „Symmetrie-Detektive“.

Es gibt noch viele Möglichkeiten…

Ihre Kreativität ist wieder mal gefragt…

Es gibt auch ein sehr schönes Spielmaterial dazu, siehe:

Interessante Spiele : Spiegeln mit dem Spiegelbuch

Weitere Praxisanregungen zur Symmetrie und zu allen folgenden Grundideen finden Sie in der Liste zu den mathematischen Grundideen.

2) Zahlenbegriff und Stellenwertdarstellung der Zahlen

Nein, die Zahlen schreiben zu können, ist zunächst nicht so wichtig.

Auch ohne diese feinmotorische Fähigkeit beschäftigen sich viele Kinder in ihrem Kopf intensiv mit Zahlen und Mengen und mathematischen Strukturen.

Literaturverzeichnis : Mittring, Gert: Was geht in uns vor, wenn wir rechnen?

Das Zahlen-Schreiben-Können und die erforderlichen feinmotorischen Fähigkeiten sollten keine Barrieren sein, um mit Kindern Mathematik zu machen. (Um zu sprechen, braucht man auch keine Buchstaben.)

Wenn Kinder Zahlen schreiben wollen, dann werden sie es von alleine beharrlich üben, sofern wir ihnen Anschauungsmaterial zur Verfügung stellen: eine Zahlentafel, Zahlen aus Pappe, Holz, Moosgummi oder Plastik, ein Zahlenpuzzle, Magnetzahlen, Zahlen zum Stempeln – was wir davon anbieten, das ist ziemlich egal, weniger ist eher mehr. Wobei jüngere Kinder Zahlen vorziehen, die nicht nur aufgemalt oder aufgedruckt sind, sondern die als Körper erfahrbar sind.

Kinder erarbeiten sich, unabhängig vom Zahlenlesen und –schreiben, früh einen Zahlenbegriff, sie wissen, dass jedes Zahlwort für eine bestimmte Anzahl von Dingen steht.

Achtung: Das ist etwas Anderes, als Zahlwörter nacheinander auswendig aufsagen zu können. Um wirklich etwas abzählen zu können, muss man die Zuordnung (siehe unten) 1 Ding – 1 Zahl kognitiv und rhythmisch (!) bewältigen. Bei ganz jungen Kindern laufen die Rhythmen des Zahlenaufsagens und des Blickens von Ding zu Ding häufig sehr schnell auseinander, und dann stimmt das Ergebnis am Ende eben höchstens zufällig.

Zum Zahlenverständnis gehört auch, dass die Kinder von den konkreten Enten, Teddybären, Bonbons abstrahieren können und die Anzahl dieser Dinge sehen. Dazu gibt es viele Vorschulübungshefte… Etliche hoch begabte Kinder kommen aber mit diesem abstrakten Zahlen-Verständnis bereits in den Kindergarten. Wenn sie zum Beispiel kein Problem damit haben, Würfelpunktzahlen in Spielschritte umzusetzen, ist klar, dass sie über einen abstrakten Zahlenbegriff verfügen.

Was ist also für diese Kinder in ihrer langen Kindergartenzeit interessant?

Zunächst mal immer größere Zahlen. Nicht wenige lernen sehr schnell, sehr weit zu zählen, und interessieren sich auch für die Struktur unseres Zahlensystems (Aufbau in Zehnerschritten) und machen sich darüber ihre Gedanken.

Wollen wir sie damit allein lassen, oder wollen wir sie dabei ein Stück weit als Partner begleiten?

Manche Kinder haben im Vorschulalter Spaß daran (und lernen natürlich viel dabei), in Zweier-, Zehner-, Fünfer- usw. Schritten zu zählen. Sie beschäftigen sich damit, rückwärts zu zählen, sie machen sich über die Beziehungen zwischen Zahlen Gedanken, zum Beispiel über die Fragen: größere – kleinere Zahl, gerade oder ungerade Zahl (nur gerade Zahlen sind durch Zwei teilbar), sie zerlegen Zahlen in kleinere Zahlen oder fügen mehrere Zahlen zu einer größeren Zahl zusammen, das heißt sie fangen an zu rechnen.

Manche Kinder benutzen dazu Hilfsmittel (Steinchen, oder was auch immer), andere vollziehen diese Denkoperationen – ganz abstrakt – nur im Kopf.

Unser Zahlensystem (und das der meisten Menschen auf der Erde) ist ein Zehnersystem (Dezimalsystem), es basiert auf der Zahl 10. Dies hat durchaus damit zu tun, dass wir Menschen 10 Finger haben. Wir zählen im Grunde immer wieder bis 10, und dann geht’s wieder von vorne los, mit dem kleinen Unterschied, dass wir bei jedem zehnten Mal die Ziffer am Anfang um Eins erhöhen.

Irgendwann im Vorschulalter entdeckt das mathematisch besonders begabte Kind noch Folgendes (oder erfasst es zumindest intuitiv): Wenn im vordersten Teil einer Zahl beim Weiterzählen aus der 9 eine 10 wird, dann wird die gesamte Zahl um eine Ziffer länger (von 9 auf 10, von 99 auf 100, von 999 auf 1000). Und so nähert es sich der Frage des Stellenwertes an.

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

usw.

91

92

93

94

95

96

97

98

99

100

101

102

103

104

usw.

111

112

113

114

usw.

Der nächste Schritt der Erkenntnis liegt nahe: Es ist wichtig, bei einer größeren Zahl den Stellenwert der einzelnen Ziffern zu beachten. Die 3 in 432 ist eigentlich eine 30, die 4 eine 400.

Das ist zunächst mal Alles.

Kein Wunder, dass sich mathematisch hoch begabte (Vorschul-) Kinder dann neuen, schwierigen Fragen zuwenden möchten, zum Beispiel: Was hat es mit Kommazahlen auf sich? Was bedeutet 17,8 Grad?

Was bedeutet 3,98 €? Was bedeutet -7? Was ist ein Achtel? Wie geht Malnehmen?

Siehe auch das Beispiel von Lena im Beitrag: Begriffsbestimmung Hochbegabung

Gibt es eine Kollegin im Team, die Spaß an Zahlenspielereien hat – oder vielleicht sogar Sie selbst??

Bitte, dann spielen Sie auch im Kindergarten mit Zahlen, zusammen mit den Kindern, die sich dafür interessieren.

3) Zuordnung und Funktion

Zuordnungsspiele gibt es im Kindergarten zuhauf. Und Kinder ordnen in einem bestimmten kognitiven Entwicklungsstadium immerzu irgendetwas zu etwas anderem zu: Das ist meins (im Sinne von: das gehört zu mir), das ist deins, das ist die Jacke von Sven, das ist die Mütze von Lina… Sie üben das Zuordnen, es macht ihnen Spaß.

Wenn wir also Zuordnungsspiele, welcher Art auch immer, beobachten oder anbieten, dann sind die Kinder dabei, Ordnung in ihr Wissen zu bringen und so „ganz nebenbei“ mathematisches Grundwissen aufzubauen. Viele bekannte Tischspiele bauen auch auf einer guten Zuordnungsfähigkeit auf (und trainieren sie gleichzeitig).

Dieses erscheint uns einfach – aber die Kinder müssen sich solche Strukturen in ihren ersten Lebensjahren erstmal erarbeiten.

Bei hoch begabten Kindern geschieht auch dieses oft sehr früh. Beispielsweise sprach ein Mädchen im Alter von 1 Jahr 9 Monaten, als es den Schokoladenweihnachtsmann der Großmutter auch noch gern aufgegessen hätte, sich selbst bremsend, die bemerkenswerten Worte: „Nee, das is Omas Puppemann.“

Ein anderes Mädchen äußerte ebenfalls mit 1;9: „Das ist Annas Hammer – nein, Annas Mamas Hammer.“

Zuordnen können ist eine Voraussetzung, um mathematische Funktionen zu begreifen. Dies sind die oft ellenlangen Ausdrücke mit vielen x, y und anderen lateinischen oder griechischen Buchstaben und mit vielen mathematischen Sonderzeichen, die uns Nicht-Mathematikern unverständlich sind.

Aber es gibt auch einfache Funktionen, die sich Kinder bereits im Kindergartenalter handelnd und denkend erarbeiten, ohne die mathematische Schreibweise zu kennen.
Zur Definition der mathematischen Funktion steht bei Wikipedia (15.8.07):

Eine Funktion f weist jedem Element einer Definitionsmenge A (einem „x-Wert“) genau ein Element einer Zielmenge B (einen „y-Wert“) zu. Eine Funktion ist also eine eindeutige Zuordnung und hat demnach die explizite Eigenschaft: Jedem x-Wert aus dem Definitionsbereich wird genau ein y-Wert zugeordnet.

Das mag sich für uns Ungeübte erstmal kompliziert lesen. (Und man könnte ja in jeder beliebigen Talkshow in Deutschland Sympathie-Punkte damit machen, wenn man sofort kategorisch erklärt: „Nein, Mathematik habe ich nie verstanden!“).

Nun gibt es ja auch extrem schwierige mathematische Funktionen, an denen 99,99 % aller Menschen verzweifeln würden – aber wir befassen uns ja glücklicherweise mit der Elementarpädagogik, und da geht es um wichtiges Basiswissen .

Jede mathematische Funktion kann als eine Gleichung mit Zahlen und Buchstaben dargestellt werden. Das heißt, auf beiden Seiten des Gleichheitszeichens kann man etwas tun, zum Beispiel etwas hinzuzählen, aber man muss es auf beiden Seiten tun, damit das Gleichheitszeichen nicht lügt.

Buchstaben werden in Gleichungen benutzt als Platzhalter für etwas Bestimmtes, oder sie können eine unbekannte Größe bezeichnen, die man noch ausrechnen will.

Die obige Definition, angewandt auf das beliebte Spiel „Schuhe in die Mitte!“ würde bedeuten:

Unsere Gruppe besteht aus 25 Kindern – alle spielen mit. In der Sprache der Mathematik sind sie die 25 Elemente einer von uns betrachteten Menge , der so genannten Definitionsmenge („x-Wert“) .

Jedem Kind – also jedem „Element dieser Definitionsmenge“ – soll nun genau ein (und zwar das richtige) Paar Hausschuhe zugeordnet werden. Die 25 Hausschuh-Paare bilden die 25 Elemente unserer Zielmenge („y-Wert“). Dabei wird von den konkreten Kindern und den konkreten Hausschuhen abstrahiert; es geht um die jeweiligen Mengen.

Beide Mengen haben gleich viele Elemente – 25 Kinder haben 25 Paar Hausschuhe. Damit gibt es für jedes Element beider Mengen genau einen passenden „Partner“, eine eindeutige Zuordnung ist also möglich und wir hätten die einfachste Funktionsgleichung überhaupt: y = x

Würden wir verlangen, dass alle Kinder 2 Paar Hausschuhe dabeihaben, dann müssten jedem Kind (Element der Definitionsmenge) zwei Paar Hausschuhe (Elemente der Zielmenge) zugeordnet werden – zweifellos eine etwas schwierigere Aufgabe. Die entsprechende Gleichung lautete y = 2x (gesprochen: Y gleich zweimal X). In Worte übersetzt: Wie viele Hausschuhpaare (y) gibt es, wenn alle Kinder (x) jeweils zwei davon haben? Bei 25 Kindern sind das 50 Hausschuhpaare. Wir haben zwar viel zu wenig Platz dafür, aber einige Kinder könnten sie vermutlich auch dann noch alle richtig den Eigentümern zuordnen.
Der Vorteil dieser Gleichungen mit x und y besteht darin, dass sie eine allgemeine Lösung des Zuordnungs-Problems ermöglichen. y = 2x funktioniert also nicht nur bei 25 Kindern, sondern auch bei 27 oder auch wenn wir die Gesamtzahl der Kinderohren ausrechnen wollen.

Manches mathematisch begabte und mathematisch empfindende Kind fühlt sich übrigens leicht geärgert, wenn Paulchen neben seinen neuen Enten-Hausschuhen auch noch seine zerfledderten Turnschuhe in die Mitte geschmissen hat. Dann geht die Funktion nämlich nicht auf, und die als schön empfundene Ordnung ist zerstört.

Solche einfachen Funktionen gibt es im Kindergarten in jedem Winkel. Jedes Kind hat einen Namen, ein Bildchen an der Garderobe, jedes Kind hat ein Eigentumsfach usw.

Wenn wir nun spaßeshalber und der Mathematik wegen feststellen wollen, auf wie viele Elemente wir kommen, wenn wir von folgenden Besitztümern der Kinder ausgehen: Jedes Kind hat genau:

1 Familiennamen (B), 2 Vornamen (C), 1 Bildchen an der Garderobe (D), 1 Jacke (E) und 2 Handschuhe (F), dann heißt die Funktionsgleichung, wobei y die Gesamtzahl der Elemente ist:

y = 1x B + 2x C + 1x D + 1x E + 2x F = 7x = 175

Wir wissen ja, dass x=25 (Kinder) ist, also ergibt sich ein Wert von y = 175 Besitztümern.

Sind nun drei Handschuhe verloren gegangen und fünf Kinder beschweren sich, weil sie eigentlich nur einen Vornamen haben, dann müssen wir die Gleichung ändern:

y = 1x B + 2x C – 5 + 1x D + 1x E + 2x F – 3 zusammengerechnet ergibt sich:

y = 7x – 8 = 175 – 8 und das sind dann

y = 167 (Besitztümer).

Was soll das Alles? Das kann ich doch auch ohne x ausrechnen!

Jaha, aber als Gleichung geschrieben, sieht es doch gleich viel mehr nach Mathematik aus! Deutlich soll werden: Mathematisches Denken durchzieht unseren gesamten Alltag, auch wenn uns das nicht immer bewusst ist. Und die Kinder ordnen ihr Denken nach Prinzipien, die auch für die Mathematik bedeutsam sind.

An der Gleichung y = a + b + c arbeitete Carolin, 4 Jahre alt, als sie Autos zählte. Die Gesamtzahl der vorbeigefahrenen Autos y war die Summe aus a (Anzahl der roten Autos) + b (Anzahl der weißen Autos) + c (Autos in anderen Farben).

Sie tat das, indem sie zunächst jedes rote Auto einem Kästchen auf ihrem Papier zuordnete, jedes weiße Auto einem anderen Kästchen und „alle übrigen“ Autos einem dritten Kästchen. Dann zählte sie die Teilmengen und danach die Gesamtmenge.

Das Beispiel finden Sie ausführlich beschrieben im Beitrag Passgenaue kognitive Förderung.

Eine interessante Anwendung der Zuordnung ist das Erfinden und Verwenden von Geheimschriften . In der einfachen Version wird jedem Buchstaben unseres Alphabets ein bestimmtes anderes Zeichen zugeordnet. Dies kann sogar wieder ein Buchstabe sein – oder eine Zahl oder ein Bildchen…

Wenn besonders oder hoch begabte Kinder dies kurze Zeit probiert haben, denken sie sich oft kompliziertere Geheimschriften aus: Das Zeichen, das an die Stelle eines Buchstabens tritt, wird nach einer bestimmten Regel gefunden, zum Beispiel: Aus dem A wird ein D, aus dem B wird ein E, aus dem C wird ein F usw. Oder das Alphabet wird einmal vorwärts, einmal rückwärts untereinander geschrieben. Ein hoch begabtes fünfjähriges Mädchen war einmal hoch aufgeregt und glücklich, als es entdeckte, dass es die untere Reihe ja auch völlig willkürlich aufschreiben könnte, zum Beispiel so:

A   B   C   D   E    F   G   H    I   J   K   L   M   N   O   P   Q   R   S   T   U   V   W   X   Y   Z
G  N   W   I   M   F   A    R   L   V   C  Q   U   H   Z    B   K   S    Y   O  X   T    P    D   E   J

„Ich muss dann aber auf meine Tabelle gut aufpassen!“ sagte sie. Besonders vergnüglich fand sie es, dass in ihrer Tabelle das F durch das F ersetzt wird. Eine wirklich raffinierte Idee für eine Fünfjährige!

Manche hoch begabte Kinder denken sich noch weit kompliziertere Systeme aus. Ein sechsjähriger (Kindergarten-) Junge weihte mich einmal in seine gerade erfundene Geheimschrift ein:

Jedem Ausgangsbuchstaben entspricht zunächst eine Zahl: Dem A entspricht die 1, dem B entspricht die 2, dem C entspricht die 3. Alle diese Zahlen werden aber quadriert, das heißt mit sich selbst mal genommen. Sein Name Thomas würde sich dann in der Geheimschrift so lesen:

400 – 64 – 225 – 169 – 1 – 361. Er war mit dem System noch nicht ganz zufrieden:

„Es muss ja nur wer merken, dass es alles Quadratzahlen sind, dann weiß er sofort, dass die 1 das A ist – und das A kommt ja dauernd vor.“

Er meinte, es würde doch sicherer werden, wenn er die 1 und die anderen kleineren Zahlen durch Primzahlen ersetzte. Primzahlen sind Zahlen, die nur durch sich selbst und durch 1 teilbar sind. Er setzte dann für das A die 37, für das B die 83, für das C die 121 und für das häufig vorkommende E die 137. Damit meinte er erstmal genug für die Verschleierung des Prinzips seiner Geheimschrift getan zu haben.

4) Teil-Ganzes-Beziehung

Dreijährige oder noch jüngere Kinder verstehen sehr oft noch nicht, was es bedeutet, wenn gerufen wird: „Kommt mal alle her!“ Entweder reagieren sie gar nicht, oder wenn sie schon eine erste Ahnung vom Begriff „alle“ haben, dann fragen sie: „Ich auch?“ Ihnen ist noch nicht recht klar, dass „alle Kinder“ auch jedes einzelne Kind meint, sie haben noch Probleme mit der Teil-Ganzes-Beziehung. Auch dies ist ein Denkmuster, das jedes Kind erst entwickeln und sich erarbeiten muss und das wiederum viel mit Mathematik zu tun hat.

Um zum Beispiel in der Mengenlehre oder in der Geometrie Schwierigeres zu verstehen, muss diese Basis erst sicher erarbeitet sein.

Selbst die einfachste Summenbildung, wie 3 + 4 = ? gelingt nur auf der (für uns Erwachsene längst selbstverständlich gewordenen) gedanklichen Basis, dass Dinge, Flächen, Mengen in kleinere Einzelteile aufgeteilt oder zu einem größeren Ganzen zusammengefügt werden können.

Ein Kind, das Puzzles zusammenfügt, beschäftigt sich mit der Teil-Ganzes-Beziehung, genauso wie ein Kind, das einen Turm baut oder einen alten Wecker auseinander nimmt. Kinder entdecken, dass es Dinge gibt, die aus gleichen Teilen zusammengefügt sind (zum Beispiel gleich große Tortenstücke auf einer Tortenplatte – das Ganze bedeutet dann nur ein „Mehr davon“), aber auch Vieles, was aus ganz unterschiedlichen Teilen besteht, trotzdem ein Ganzes ergibt, das aber dann eine ganz andere Qualität und einen ganz anderen Gebrauchswert gewinnt (wie zum Beispiel der Wecker).

Komplexes analytisches und synthetisches (im Sinne von Synthesen bildendes) mathematisches Denken findet in diesen kindlichen Entdeckungen wiederum seine notwendige Basis.

5) Algorithmen

Vor diesem aus dem Arabischen stammenden Wort muss man sich nicht fürchten.

Unter einem Algorithmus versteht man allgemein eine genau definierte Handlungsvorschrift zur Lösung eines Problems oder einer bestimmten Art von Problemen in endlich vielen Schritten. (Wikipedia 15.8.07)

Koch- und Backrezepte sind im Prinzip Algorithmen. Dabei ist interessant, dass schwer anzugeben ist, wie ausführlich ein Algorithmus sein muss. Im alltäglichen Leben, bei Rezepten zum Beispiel, wird oft zu viel vorausgesetzt: Im Rezept steht zum Beispiel nicht, dass man den Topf auf den Herd stellen und den Herd anstellen muss, dass man dann beobachten muss, wann die Speise heiß ist, um dann den Herd wieder runterzuschalten… Dort steht nur „erhitzen“.

Dies ist eins der Grundprobleme von Rezepten, Bedienungsanleitungen und Pädagogik: Wie viel kann ich voraussetzen, wie viel muss ich erklären?

Muss ich hinschreiben, dass man den Stecker in die Steckdose stecken muss, um ein elektrisches Gerät in Gang zu bringen? Oder kann ich das voraussetzen? Oder fragt sich der ungeübte Koch bei „erhitzen“ vielleicht hilflos: „Ja, wie denn? In der Pfanne, im Topf, im Backofen, und woran merke ich denn, ob es schon heiß genug ist?“

Ebenso geht es Kindern andauernd: „Wisch mal den Tisch ab!“ Aber was, wenn der Algorithmus für Tischabwischen dem Kind noch gar nicht bekannt ist? Dann hat es keinen Plan und wird vielleicht lustlos und unsicher einmal mit dem Ärmel über den Tisch fahren. Aber wir hatten ganz andere Vorstellungen (einen anderen Algorithmus): Lappen holen (wo?), Lappen nass machen (wo und wie?) und (genügend) ausdrücken, den Tisch frei räumen (wohin mit den Gegenständen?), den Tisch vollständig (gar nicht so einfach) abwischen und evtl. mit einem trockenen Tuch (ebenfalls die ganze Tischfläche) nachwischen. Lappen und Tuch wieder wegräumen (wohin?).

Es ist nicht schlecht, im dritten Lebensjahr das Programm im eigenen Gehirn zu starten: „Wie ich einen Tisch mit einem feuchten Lappen so abwische, dass er hinterher sauber ist.“ Dies kann man später brauchen, wenn man mit 11 Jahren kreativ kochen will, ohne dass die Eltern es wegen völliger Einsauung der Küche fürs nächste Mal verbieten…

Es gibt wenige 11-jährige Kinder, die Lust haben zu lernen, wie man einen Tisch richtig abwischt, mit zwei bis drei Jahren dagegen machen es viele Kinder gern und mit Feuereifer.

Je mehr Jemand schon kann, desto kürzer kann der Algorithmus sein. Dies ist auch bei Computerprogrammen so. „Kennt“ der Computer schon viele hilfreiche Programme, verfügt er zum Beispiel über ein ausgefeiltes Betriebsprogramm mit vielen Unterprogrammen, dann kann das Schreibprogramm darauf aufbauen, indem es auch schon Vorhandenes anpasst und neu kombiniert. Auch mathematische Algorithmen können oft noch kürzer und „eleganter“ werden, je mehr Mathematik der Rechner (egal ob Mensch oder Maschine) schon versteht.

Um souverän und selbstständig handeln zu können (in welchem Bereich auch immer), muss das Kind in seinem Gehirn erst viele, viele einfache Algorithmen einbauen und „verdrahten“, die es dann zu komplexeren Tätigkeiten („Ich decke mal den Tisch und wische ihn vorher schnell ab!“) zusammensetzen kann.

Solche Algorithmen (genauen Ablaufpläne) im Kopf zu haben und ausführen zu können, das bedeutet, über Fähigkeiten und Fertigkeiten zu verfügen. Durch das praktische Ausführen klärt sich der Algorithmus im Kopf; Fehler, Irrwege und Umwege werden eliminiert (wie bei so genannten „Bananenprogrammen“ für den Computer, die so heißen, weil sie erst beim Benutzer reifen). Andererseits führt ein klarer und von Fehlern befreiter Algorithmus zu zügigem Erfolg, er wird häufig sogar weitgehend automatisiert; dadurch wird der Kopf frei für neue Strategien und für kreative Ideen.

Leider passiert hier in vielen Familien viel zu wenig . Das wirkt sich so aus, dass die Kinder schrecklich unselbstständig sind und nur wenig „können“. Andererseits gibt es auch gut geförderte „Könner“, denen alles leicht von der Hand geht, die sich mit drei Jahren ein Brot schmieren können, eine Blume einpflanzen können, die mit fünf Jahren wissen, wie man sicher über eine Straße kommt, die Streit schlichten können, die Spielregeln vereinbaren können, usw.

Planvolles Handeln lernt man nur durch planvolles Handeln. Hier hat der Kindergarten wieder ganz viele Pluspunkte: Den Kindern wird Selbstständigkeit abverlangt, Selbstständigkeit ist hier ein hoher Wert, die Kinder lernen zum Beispiel, mit immer mehr Plan und Übersicht zu bauen und zu basteln… Je mehr die Kinder zum Planen angeregt werden, wozu auch gehört, Pläne den Gegebenheiten anzupassen, das Ergebnis zu kontrollieren, desto besser.

Indem wir gewohnheitsmäßig noch einmal die Arbeitsschritte gemeinsam reflektieren, wenn der Ablauf den Kindern noch nicht wirklich vertraut ist, machen wir die zu Grunde liegenden Algorithmen bewusst und tun damit viel für die Selbstständigkeit und zugleich für die mathematische Grundbildung der Kinder. Kinder, die so früh wie möglich auch zu Hause im Haushalt, im Garten, beim Heimwerken oder bei anderen ergebnisorientierten Tätigkeiten mithelfen dürfen und gut angeleitet werden, sind hier im Vorteil.

Sie erarbeiten sich auch eine notwendige Basis, um später gute Algorithmen ausdenken zu können, zum Beispiel „Wie bereiten wir unsere Hochzeit vor?“ – oder aber auch Computerprogramme, Rezepte oder Bedienungsanleitungen, wobei natürlich andere wichtige Fähigkeiten und Talente hinzukommen müssen.

6) Messung

Was kann man Alles messen? Und wie geht das? Und wozu tut man es?

IHVO-Kursteilnehmerinnen, die sich mit interessierten Kindergartenkindern auf diese Fragen gestürzt haben, waren begeistert, wie intensiv, klug und ausdauernd die Kinder bei der Sache waren.

Vom einfachen (für kleine Kinder ist es natürlich wieder neu) Messen von Längen, Breiten und Höhen ging es weiter zum Gewichte messen, Temperaturen messen, Zeit messen, Rauminhalte messen. Die Messungen gingen über in technisches Bauen und Basteln, in philosophische Fragen (Was ist Zeit? Was ist Unendlichkeit?), in gesundheitsvorsorgerische Maßnahmen (die Kühlschranktemperatur kontrollieren, vorsorglich Fieber messen, ehe der Kindergarten betreten werden darf, diese Schuhe sind zu klein)…

Auch hier ist es wieder eine gute Methode, die einfachen Prinzipien des Messens möglichst vielen Kindern nahe zu bringen, und dann zu gucken: Welche Kinder wollen / brauchen mehr? Dabei funktioniert es oft nicht gut, mit allen Kindern erstmal gaaanz einfach und laaangsaaam zu beginnen und darauf zu vertrauen, dass die schnelleren und wissbegierigeren Kinder das geduldig abwarten und dann noch weitermachen wollen. Oft wandern sie dann äußerlich oder innerlich schon ab.

Als bessere Idee hat sich erwiesen, zunächst mit den (in diesem Bereich) schwächeren Kindern zu beginnen und zu sehen, wie weit sie interessiert sind und wie weit sie gehen können und wollen – und sich dabei auch für die einfachen Dinge die nötige Zeit zu lassen. Mit den (in diesem Bereich) stärkeren (begabteren, schon fähigeren, wissenderen, motivierteren) Kindern kann man dann noch mal gesondert in das Thema starten und die einfachen Dinge im Schnelldurchgang „erledigen“ oder gleich überspringen und sich den schwierigeren Fragen zuwenden.

Zum Beispiel: Wie kann man messen, welcher von zwei etwa gleichgroßen Steinen nun wirklich der größere ist? Was heißt jetzt größer: höher, breiter, oder mehr Masse, mehr Rauminhalt? (Tipp: Wasserverdrängung messen.) Und welcher ist schwerer? (Wenn wir beides, Rauminhalt und Gewicht mehrerer Steine vergleichen, dann führt uns das zur Frage der Dichte.)

Ein Verständnis für Messwerte und Messmethoden zu entwickeln, weitet den Horizont für mathematische Fragen, aber auch für naturwissenschaftliches Forschen.

Messgeräte für die Kita anzuschaffen, die Kinder damit vertraut zu machen und sie für die Kinder zugänglich zu halten, hat sich bewährt. Lineal, Schneider-Maßband, Zollstock, Messbecher, Thermometer (ohne Quecksilber), verschiedene, auch selbstgebaute Uhren (Sonnenuhr, Wasseruhr…), verschiedene Waagen (Küchenwaage, Briefwaage, Marktwaage mit zwei Waagschalen und Gewichten).

Das Alles fasziniert viele Kinder.

Siehe auch: Die Zahlendetektive messen.

7) Näherung, Schätzung

Es gibt bei Sommerfesten manchmal diese interessanten Wettspiele: Wie viele Erbsen / Murmeln / Steinchen sind wohl in diesem Glas? Wer mit seiner Schätzung am nächsten dran ist, gewinnt einen Preis. Oft merken wir dann erst, wie schlecht wir schätzen können. Vielen Menschen sagt es auch wenig, wenn ihnen Jemand Auskunft gibt: „Na, das sind noch so etwa 800 Meter bis zum Bahnhof.“

Alles, was man zählen oder messen kann, kann man auch schätzen: Anzahl, Gewichte, Geschwindigkeiten und Windstärken, Temperaturen, Längen und Entfernungen, Höhen und Tiefen, Helligkeiten, Lautstärken, Festigkeiten von Materialien, Zeitspannen, Formen (das ist ungefähr eine Kugel)…

Was hat das mit Mathematik zu tun, und warum sollen Kinder es lernen?

Es ist sinnvoll, möglichst früh ein Gefühl für Geschwindigkeiten, für Mengen usw. zu entwickeln. Es erleichtert die Orientierung und gibt Sicherheit im Handeln. Wüsste ich, dass der Auskunftgeber (800 Meter bis zum Bahnhof) sich in der Stadt auskennt und gut Entfernungen schätzen kann, und wüsste ich noch, wie viele Meter ich ungefähr in 1 Minute gehen kann, dann könnte ich schnell schätzen, ob ich mich entspannen kann oder ob ich lieber rennen sollte, um den Zug noch zu kriegen.

Auch ist es hilfreich, wenn man überschlagsmäßig berechnen kann, wie viel ungefähr die Rechnung im Restaurant betragen könnte, um eventuelle größere Irrtümer sofort zu bemerken. Größenordnungen einschätzen zu können, ist im alltäglichen häufig wichtig und nützlich.

Aber auch die wissenschaftliche Mathematik, die Wirtschaftsmathematik, die Statistik usw. arbeiten mit Schätzungen und Näherungen, dies spart oft viel Zeit und Geld ein und führt oft zu hinreichend guten Ergebnissen.

******************************************************

Was hoch begabte Vorschulkinder an der Mathematik auch früh interessiert:

Pläne (Stadtpläne, Landkarten, Konstruktionspläne…) lesen;

eben Alles, wo man sich auf recht abstakte Weise orientiert, um sich in der konkreten Wirklichkeit besser zurecht zu finden.
Natürlich ist auch das Ausdenken und Zeichnen von Plänen und Skizzen für viele hoch begabte Vorschulkinder hochinteressant und hoch lehrreich.
Näheres dazu Pläne, Zeichnungen, Skizzen, Mind-Maps

Über Wahrscheinlichkeiten und über den Zufall nachdenken.

Das Konzept Zufall ist für kleine Kinder recht schwierig zu begreifen. Haben sie doch genug damit zu tun gehabt, erstmal zu verstehen, dass es offenbar für Alles eine Ursache gibt und das Geschehen in der Welt aus Ursachen und ihren Wirkungen zusammengesetzt ist. Und so neigen sie nun auch erst mal dazu, auch für zufällige Ereignisse Jemandem „die Schuld“ zu geben. Irgendwann zündet dann die nächste Stufe der geistigen Entwicklung und das Kind begreift, dass es Dinge gibt, die zufällig geschehen, das heißt auch schwer vorhersehbar und nicht beeinflussbar sind. Zufällige Ereignisse kann man nur abwarten.
Siehe auch: Beispiel für großes Interesse an Systematik und logischen Zusammenhängen. (Das Beispiel von Daniel und dem Adventskalender, veröffentlicht am 30.10.08.)

Wenn ein Kind sehr früh, etwa mit drei bis vier Jahren, bereits über ein solches Programm verfügt, kann dies dazu führen, dass es von seiner Umwelt als besonders ängstlich wahrgenommen wird. Näheres dazu unter Ängstlichkeit und Vor-Sicht bei hoch begabten Kindern .

Die Null.

Die Null ist noch jung. Inder, Babylonier, Ägypter, Chinesen, Griechen und andere Völker kannten schon vor etlichen tausend Jahren Zahlen und hatten eine hohe Mathematik entwickelt. Aber die Null wurde erst um 500 unserer Zeitrechnung erfunden. Erst im 11. Jahrhundert wurde sie allmählich in Europa bekannt.

Was an der Null so schwierig ist, lässt sich bei hoch begabten Vorschulkindern nicht ausmachen: Sie gehen mit der Null ganz locker um. Erst wenn sie zum Dividieren (Teilen) kommen, wird es spannend, denn durch Null teilen „geht nicht“. Man erhält jedenfalls keine bestimmte Zahl als Ergebnis, sondern das Ergebnis ist immer unendlich.

Tipp:

Im Museum „Arithmeum“ in Bonn (mit guten Kinderführungen, auch für an Zahlen und am Rechnen interessierte ältere Kindergartenkinder geeignet) kann man viel über die Geschichte und die Techniken des Rechnens erfahren.

http://www.arithmeum.uni-bonn.de/

Bilderbücher / Kindersachbücher zum Thema Zahlen und Mathematik:

Zahlenmärchen.

Von Ida Fleiß und Gert Mittring. Wagner Verlag.

Es gibt inzwischen etliche Bilderbücher, die sich mit dem Zahlenraum von 1 bis 10 befassen, den sich hoch begabte Kinder oft schon im zweiten und dritten Lebensjahr erobern. Dieses Buch greift weiter und höher und ist dementsprechend auch für Mathe-Spezis unter den älteren Vorschulkindern interessant.

Es ist ein Märchenbuch, das im Zahlenland spielt. Die Kinder werden von Gert, dem Weltrekordler im Kopfrechnen, zu einem interessanten Ausflug eingeladen. Sie besuchen die Zahlenklinik, die Zeichenfabrik, das Café mit Ziffernkaffee und Wurzeltorte, sie fahren nach Neunerstadt und besuchen dort das Zahlenmuseum und schließlich gelangen sie noch zur Zahlenhöhle.

Während der Zugfahrten von Ort zu Ort hören sie spannende Märchen:

Die Zahlenspinne

Wie die Drei liebe Freundinnen fand

Der verliebte Dino

Das Märchen vom König Teilbarkeit dem Zweiten

Das Geheimnis der tanzenden 8

Der Träumeverkäufer

Der Teufel und die Zahlenhexe

Das Märchen von der schlauen 5

… und immer geht es um Zahlen.

Jedes Märchen kann für sich (vor)gelesen werden, ebenso jede Station auf der Reise. So können sich Kinder den Inhalt des Buches auch nach und nach erschließen.

Ein Buch für Kindergarten- und Grundschulkinder, die Zahlen als Freunde betrachten und sich aus eigenem Antrieb viel mit ihnen befassen.

Das Bilderbuch von den Zahlen

von Rolf und Margret Rettich, Ravensburger Verlag

Dies ist ein Bilderbuch für den Zahlenraum von 1 bis 10, daher vielleicht für junge hoch begabte Vorschulkinder interessant.

Kindergartenspaß mit Willi Wiesel. Zählen und Tüfteln.

Ensslin Verlag.

Ein Arbeitsheft zum Zählen und Ausmalen. Umfasst ebenfalls nur den Zahlenraum von 1 bis 10. Also: Nicht zu spät damit ankommen!

Komm mit ins Zahlenland. Eine spielerische Entdeckungsreise in die Welt der Mathematik

von Gerhard Friedrich und Viola de Galgóczy.

Ein didaktisch aufbereitetes Spiele- und Geschichtenbuch für den Zahlenraum von 1 bis 10. Gut geeignet für den Kindergarten. Für zwei- bis vierjährige Hochbegabte interessant, wenn sie grade dabei sind, den Zahlenraum bis 10 zu begreifen, danach vermutlich nicht mehr spannend.

Was ist Was, Band 12: Mathematik

Tessloff Verlag

Das Buch enthält viele gute Abbildungen und Erklärungen, auch zum Nachlesen für die Erzieherin wichtig

Die Übersetzung dieses Beitrags ins Englische
wurde gesponsert von
Jordis Overödder, Kürten.

 

Copyright © Hanna Vock 2007, siehe Impressum.
Datum der Veröffentlichung 4.9.07 /Version März 2011

Projekt: Zeit

Posted on by

– Kinder setzen sich mit der Zeit auseinander –

von Klaudia Kruszynski

 

Am Anfang stehen die Vorüberlegungen und Ideen zum Durchführen eines Projektes im Kindergarten.

Was tatsächlich realisiert wird, wird den Kindern überlassen – Änderungen und Abweichungen sind möglich. Auch der Zufall und der Alltag können die Durchführung beeinflussen.

…kurz gefasst…
Der Beitrag beschreibt ein langfristiges Projekt, in dem sich Kindergartenkinder intensiv mit der Zeit auseinandersetzen. Es werden alle Entwicklungsbereiche und Sinne angesprochen, im Zentrum steht mathematische Grundförderung, die die Lernbedürfnisse der hoch begabten Kinder in hohem Maße berücksichtigt.
Verschiedene Projekte bauen in der mathematischen Förderung aufeinander auf, auch wenn das auf den ersten Blick nicht auffällt.

Inhalte des Projekts:

1) Wahrnehmung der Zeit
Vergehen der Zeit bewusst erleben,
zum Beispiel: Wie verändern sich Pflanzen (Blumen) mit der Zeit? Wie verändern sich Menschen mit der Zeit? Was sind Jahreszeiten?

2) Wie kann man Zeit messen?
Experimente, Zeitmesser bauen (Ideen der Kinder), Uhren – verschiedener Arten

3) Was schafft man in einer Minute?
Experimente, Vergleiche, Abläufe dokumentieren (Algorithmen)
Siehe auch: Grundideen der Mathematik

4) Erstellen einer Zeitlinie
Wann war gestern, vorgestern? Wann ist morgen? Was ist morgen am Morgen? Usw.

5) In die Zukunft denken:
Was heißt es:
Ich räume später auf?
Das Bild möchte ich lieber morgen malen.
Was mache ich nächste Woche, zu Weihnachten?
Was mache ich, wenn ich groß bin?

6) Besondere Zeiten: zum Beispiel Advent
Adventskalender, Adventskranz
Jahreswende, Jahresende, Neujahr
Kalender, Monate, ‚Wochen, Tage
Namen der Monate, Wochentage.

7) Wichtige Begriffe:
schnell – langsam, früh – spät, kurz – lang, jetzt – später, immer – nie, selten – häufig – usw.

8 ) Mögliche Experimente:
Was schafft man in einer Minute?
Wie viel schafft man, wenn man die Tätigkeiten schneller/langsamer durchführt?
Wie weit geht man in einer Minute?
Wie viele Schritte macht man in einer Minute? (Unterschiede: große, kleine Kinder; langsame und schnellere Kinder)

Wichtiger Entwicklungsschritt: Zeitabläufe

Was muss ich alles nacheinander tun, um etwas zu machen(schaffen), zum Beispiel
um die Zähne sauber zu bekommen, um einen Kuchen zu backen, um Hände sauber zu bekommen.

Wie lange dauert das?

Dokumentation:

gemalte Bilder, Fotos, Listen, Mappen, usw.

Die Kinder:

Die ausgewählten Kinder waren (alle Namen geändert):

Tim, 5 Jahre 3 Monate
Jan, 4 Jahre 1 Monat
Mark, 5 Jahre 1 Monat
Linea, 4 Jahre 2 Monate
Lukas, 4 Jahre 6 Monate
Anna, 3 Jahre 3 Monate
Julius, 5 Jahre 11 Monate
Sven, 3 Jahre 11 Monate

Wie kamen wir auf dieses Thema?

Die Beobachtung von Tim gab für mich den Anstoß. Ich überlegte, in wie weit ich auch bei anderen Kindern Interesse am Phänomen Zeit erkennen konnte.

Tim

Er kann schon ziemlich gut die Uhr lesen, die vollen Stunden, die halben und Viertelstunden. Für die anderen Zeiten benutzt er Bezeichnungen wie: ein bisschen nach oder vor.

Er kann seine Zeit nicht richtig einschätzen, er frühstückt sehr lange (manchmal bis zu 1 Stunde, wobei das Essen nur wenige Minuten dauert), beim An- und Umziehen ist er fast immer der letzte, genauso ist es beim Aufräumen.

Auf der anderen Seite beschwert er sich, dass er immer nur kurz spielen darf, dass die Bauecke immer besetzt ist.

Ich weiß, dass er schon zu Hause sehr lange braucht, bis er fertig ist. Er könnte viel eher im Kindergarten sein, aber er findet immer etwas, was ihn vom Anziehen, Waschen und Frühstücken ablenkt.

Vor einer Woche kam er wieder sehr spät in den Kindergaten. Seine Mutter sagte uns, dass er zu Hause geweint hat und nicht in den Kindergarten gehen wollte, weil er schon sehr, sehr lange nicht in der Bauecke gespielt hat. Er meinte, die Bauecke wäre immer schon voll. Es sei sehr gemein, dass er da nie spielen darf. Er gab uns die Schuld.

Wir hörten uns seine Beschwerde an und sagten, dass wir es verstehen, dass er so unzufrieden ist. Wir überlegten, wieso er nicht n der Bauecke spielen kann. „Da sind immer andere drin“. „Wieso?“ „Weil sie schon früh im Kindergarten sind“. „Kannst du auch früher in den Kindergarten kommen?“ Seine Mutter nickte, und er sagte „Ja“.

Für diesen Tag haben wir abgemacht, dass er zuerst frühstückt und danach in die Bauecke gehen darf. Um halb zehn war die Bauecke noch frei, aber Tim saß am Frühstückstisch bis 20 nach 10. Wir haben ihn mehrfach erinnern müssen, dass er weiter frühstückt, er unterhielt sich mit den Kindern, beobachtete, was die anderen tun, träumte, schaute zum Fenster hin, spielte mit seinem Essen usw. bis er auch mit dem Zähneputzen fertig war, war es schon kurz vor elf.

Genauso ist es beim Malen oder Basteln. Die reine Tätigkeit dauert bei Tim nicht länger als bei den anderen Kindern, er hat auch keine Schwierigkeiten bei der Durchführung. Aber er verliert sehr viel Zeit durch verschiedene Ablenkungen, und schließlich verliert er auch die Lust weiter bzw. zu Ende zu arbeiten.

Dies bereitet uns Sorgen. Er könnte früher eingeschult werden, er würde den Stoff in der Schule gut begreifen, gut rechnen, viel wissen beweisen, aber wie würde es mit dem selbstständigen Arbeiten klappen? Würde er mitkommen? Was passiert, wenn langweilige oder langwierige Aufgaben gelöst werden müssen?

Tim weiß, dass er viel Zeit verliert, er möchte flott sein, nur es klappt nicht immer.

Ich habe mir überlegt, dass ich ihm bewusst machen kann, wie die Zeit vergeht. Dass er lernen könnte, selber wahrzunehmen, was geschieht, wann er sich auf sein Tun konzentriert und wann er sich davon entfernt.

Jan

Manchmal hat er ähnliche Probleme mit der Zeit wie sein Freund Tim. Außerdem interessiert er sich für alles, was mit Mechanik zu tun hat. Vielleicht hat er eine Idee, wie die Uhr funktioniert? Er macht auch gerne verschiedene Versuche. Er diskutiert gerne, entwickelt eigene Ideen, hat sehr viel allgemeines Wissen.

Mark

Er könnte sehr viel Spaß an den Experimenten und Versuchen haben. Er hat auch viel Wissen, aber er zeigt es ungern. Ich hoffe, dass er im Spiel seine Hemmungen vergisst und mehr Selbstvertrauen gewinnt.

Lukas

Er ist neu in unserer Gruppe, war schon ein Jahr in einem anderen Kindergarten. Er hat Sprachprobleme: undeutliche Artikulation und falscher Satzbau. Er denkt sehr schnell, macht sehr große Puzzle-Spiele, malt Unmengen an Bildern. Er ist sehr konzentriert bei den Aufgaben, zielstrebig (manchmal trickst er, um sein Ziel zu erreichen) und ausdauernd im Verlangen nach Mandala-Bildern. Er hat noch keinen Freund gefunden, spielt meistens alleine oder mit den Erzieherinnen. Er wird von den Kindern nicht richtig verstanden, auch Erwachsene verstehen ihn schwer.

Ich hoffe, dass er durch das gemeinsame Experimentieren mehr Kontakte zu den anderen Kindern bekommt und seine Scharfsinnigkeit das Projekt bereichern wird.

Linea

Wenn sie etwas malt oder bastelt, ist sie dabei sehr ausdauernd, in jungem Alter von 3 Jahren und 10 Monaten interessierte sie sich für ein Projekt „Schule spielen“ und hat alle Arbeitsblätter ausgefüllt. In der gleichen Zeit stickte und webte sie, ihre Ergebnisse konnte man mit denen der Sechsjährigen vergleichen. Sie ist sehr vernünftig – sie benutzt die Argumente der Erwachsenen und steht dahinter, z.B. „Man darf die Zahnbürste nicht aus Spaß vertauschen, weil man sich mit Schnupfen anstecken kann, man macht das einfach nicht!“

Sie interessiert sich sehr für Buchstaben und Zahlen, liebt außergewöhnliche Aufgaben (etwas später, mit 4 Jahren, erstellte sie ein Bilderbuch). Sie möchte die Uhr lernen.

Anna

Sie ist das jüngste Kind in unserer Gruppe. Sie freundete sich mit Linea an. Sie beobachtet genau alles, was im Raum geschieht, nimmt gerne an allen Angeboten teil. Sie redet wenig – man könnte denken, sie wäre sehr schüchtern. Zu Hause erzählt sie detailliert, was die Erzieherinnen gesagt/gemacht haben, ebenso, was die Kinder gemacht haben. Bei allen Tätigkeiten erzielt sie Ergebnisse wie die älteren Kinder, sie ist schon längst selbstständig und natürlich auch sehr vernünftig.

Einstieg in das Projekt

Donnerstag, der 11.11.04:
Tim, Jan und Ahmed wollen gemeinsam frühstücken. Ich frage sie, ob sie wissen möchten, wie lange sie essen. Ich zeige ihnen die Stoppuhr und erkläre, wie sie funktioniert. Das möchten die Kinder. Auf mein Zeichen fangen sie an, und ich starte die Uhr. Ich sage den Kindern, dass wir es aufschreiben, wie lange es bei Jedem dauert. Die Kinder essen wie immer, in eigenem Tempo. Ich erinnere sie nicht daran, dass sie weiter essen. Dieses Messen möchten wir jeden Tag fortführen.

Eine kleine Gruppe Kinder trifft sich im Nebenraum. Dabei sind: Tim, Jan, Mark, Lukas, Kris, Jane, Linea, Kim, Carolin. Ich zeige den Kindern die Stoppuhr. Manche wissen es schon, was man mit der Stoppuhr machen kann. Wir beschließen es auszuprobieren.

Diese Uhr hat mehrere Funktionen, sie zeigt die Tageszeit an, kann als Timer benutzt werden und als Stoppuhr. Wir probieren diese Funktionen aus.

Man kann z.B. sehen, wie lange ein Minute dauert. Ich frage die Kinder, ob sie wissen, wie lange eine Minute dauert? Die meisten sagen „Ja“. Dann machen wir einen Versuch: ich stelle den Timer auf eine Minute, die Kinder sollen ihre Augen so lange geschlossen halten, wie sie glauben, dass eine Minute dauert. Ich drücke „Start“. Manche Kinder öffnen ihre Augen schon nach ein paar Sekunden, einige halten sie lange geschlossen. Ich huste einmal, als die Minute um ist. Die letzten Kinder öffnen die Augen. Dann frage ich sie, ob sie es gehört haben, wie ich gehustet habe – da war die Minute gerade vorbei. Sie lachen.

Beim zweiten Versuch sollen sie nur auf der Uhr beobachten, was sich verändert, wenn die Zeit läuft. Sie merken sofort, dass die Eins verschwunden ist und die Zahlen ändern sich. Einer sagt, die Zahlen werden immer kleiner. Bei der Null piepst die Uhr. Danach benutzen wir die Stoppuhrfunktion, wir fangen bei 0:00 an. Die Kinder zählen mit, sie sehen, dass nach 0:59 eine 1:00 kommt. Tim und Jan wissen, dass es Sekunden waren, die immer mehr geworden sind.

Jan sagt auch, dass die Uhr einmal vorwärts und einmal rückwärts gelaufen war. Man kann mit der Stoppuhr messen, wie lange etwas dauert. Wir singen das Lied: „Laterne, Laterne, Sonne, Mond und Sterne“. Danach hat Tim abgelesen, wie lange es gedauert hat: 18 Sekunden. Wir wiederholen den Versuch, es dauert 19 Sekunden. Danach singen wir sehr schnell – 13 Sekunden sind nur vergangen. Zum Schluss singen wir sehr langsam, es dauert 24 Sekunden. Die Kinder finden es sehr faszinierend, sie möchten noch andere Versuche machen.

Einer schlägt vor, dass wir messen können, wie lange man sich ein Bilderbuch anschaut. Tim meldet sich als erster. Er öffnet das Buch, Jan startet die Uhr. Tim fängt an zu lesen (!). Alle sind überrascht, einige Kinder freuen sich, manche werden sehr ernst. Obwohl die Aufgabe anders war, lasse ich ihn das Buch zu Ende lesen. (Wenn man Tim darum bittet etwas vorzulesen, blockt er sofort ab, hat keine Lust oder er sagt, er kann noch nicht lesen.) Bei manchen schwierigen Wörtern helfe ich ihm. Tim benutzt beim Lesen verschiedene Techniken: Er buchstabiert, er liest kurze Wörter wie „die“ oder „in“ auf einmal, manche Wörter rät er vom Sinn der Geschichte. Oft verwechselt er „d“ mit „b“. Nach 9 Minuten und 50 Sekunden ist er fertig. Danach lese ich die Geschichte noch mal, es dauert 1 Minute und 21 Sekunden.

Die Kinder verlassen den Nebenraum, Jan hilft mir beim Aufräumen. Er sagt, er kann auch schon die Buchstaben und singt „A,b,c,d,e,f,g,h,i,j,k,l,m,n,o,p,q,r,s,t,u,v,w,x,y und z“. bis jetzt hat Jan immer abgestritten, dass er die Buchstaben kennt, oder er meinte, dass er sie erst in der Schule lernen wird. (Ich habe schon vor einem Jahr beobachtet, dass er die Buchstaben kennt).

Es war deutlich zu sehen, dass das Vorlesen von Tim auf ihn einen großen Eindruck gemacht hat. Ich kann es mir vorstellen, dass er auch bald lesen wird. Sein Motiv wird wahrscheinlich die Tatsache sein, dass sein bester Freund es schon kann.

Freitag, der 12.11.04:

Wir messen wieder die Zeit, die Jan, Tim und Ahmed zum Frühstücken brauchen. Ich schreibe sie auf. Ich habe beschlossen, dass ich einen Bogen entwerfen muss, worauf die Kinder selbstständig ihre Zeiten eintragen können. Zusätzlich sollen sie aufzeichnen, was sie zu essen hatten. Nach mehreren Versuchen könnten wir uns die Bögen anschauen und überlegen, wieso die Zeiten verschieden sind.

Später trifft sich die Gruppe im Nebenraum. Es sind auch andere Kinder dabei. Ich habe drei verschiedene Uhren dabei, die von gestern, eine Sport-Stoppuhr und einen Reisewecker. Die Kinder schauen sich die Uhren an, manche haben sie vorher schon woanders gesehen. Ich frage, wodurch sie sich voneinander unterscheiden. Sie erkennen, dass zwei nur die Zahlen zeigen – ich sage, es sind Digitalanzeigen. Die dritte Uhr hat Zeiger.

Welche Zeit zeigen die Uhren? Jan, Tim und Mark sagen: 11 Uhr 12.
Was zeigt die dritte Uhr?
Erst jetzt entdecken die Kinder, dass diese Uhr eine andere Zeit zeigt. Die Zeiger bewegen sich nicht. „Wieso?“
„Sie ist kaputt. Nein, da ist keine Batterie drin!“

Ich frage die Kinder, ob sie mit mir „Die Zeitdetektive“ spielen wollen? Diese Idee gefällt den Kindern, obwohl sie noch nicht wissen, was die Zeitdetektive tun. So fängt unser Projekt „Zeit“ an.

Zeit, Tempo, Rhythmus, Reihenfolge

Dies ist ein Turnangebot für Kinder von 3 bis 6 Jahren

Ziele:

Erkennen und Unterscheiden von verschiedenen Geschwindigkeiten: langsam, schell
Durchführen von verschiedenen Bewegungen in unterschiedlichen Geschwindigkeiten.

Schätzen und Ausprobieren, wie lange es dauert eine Tätigkeit (Bewegung) durchzuführen, auch mit dem unterschiedlichen Tempo.

Messen der Zeit, die man für die Durchführung braucht, aufschreiben.

Schützen und Ausprobieren, was man in der Zeit von 1 Minute schafft, wie weit man gehen, springen, krabbeln, usw. kann.

Merken einer bestimmten Reihenfolge der Aufgaben, durchführen, Zeit messen, aufschreiben.

Aufgaben für die Zeitdetektive:

  • Bedienen (Benutzen) der Stoppuhr,
  • Messen und Aufschreiben der Zeiten,
  • Helfen bei der Durchführung der Turnstunde,
  • Verteilen der Gegenstände,
  • Entwickeln der Aufgaben.

Gegenstände, Hilfsmittel:

Stoppuhr
Kärtchen mit Zeichen: Schnecke, Igel, Hase
Häuserzeichen
Tamburin
Messtabellen, Stifte, kleine Zettel
Turnbank, Kasten, Hütchen, usw.

Spiele:

  • Langsam – schnell: laufen, springen, klatschen, stampfen – Tamburin
  • „Was bin ich?“- Kärtchen mit Tiersymbolen, Häuschen, Stoppuhr : die Kinder bekommen Kärtchen mit Tiersymbolen. Auf ein Zeichen bewegen sie sich so schnell, wie die abgebildeten Tiere es tun. Die Zeitdetektive müssen erkennen, welches Tier jedes Kind ist und in das richtige Häuschen führen, dabei kann die Zeit gemessen werden. Danach werden die Kärtchen kontrolliert.
  • Wie lange dauert es, bis eine „Schnecke“, „Igel“ oder „Hase“ durch die ganze Turnhalle gelaufen sind – Stoppuhr, Kärtchen, Stifte .
  • Wie weit laufen die „Tiere“ in der Zeit von 1 Minute – Diagramme, Stifte .
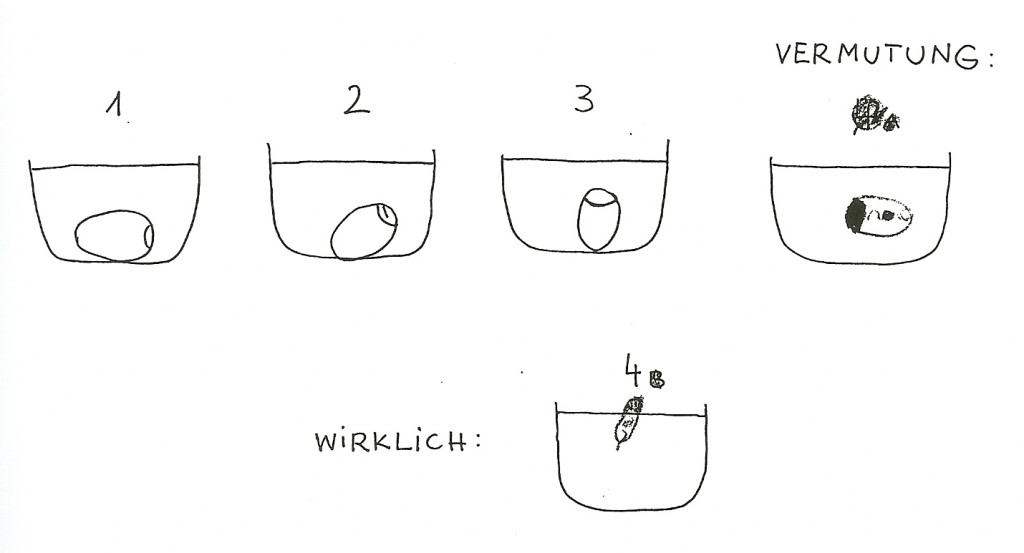
  • Eine Spielgeschichte: „Wir gehen angeln“. Ziel des Spieles ist einen Fisch in den Topf zu werfen. Vorher müssen verschiedene Aufgaben erfüllt werden, dabei ist die Reihenfolge wichtig: aus dem Kasten muss die Angel rausgeholt werden, die Stiefel müssen angezogen werden, ein Eimer muss mitgenommen werden, dann geht es über eine Brücke (Bank) zu dem See ( blaues Tuch ), ein Fisch wird gefangen, in den Eimer geworfen, dann zurück über die Brücke, die Stiefel ausziehen, die Angel in den Kasten zurücklegen und den Fisch in den Topf werfen. Die Zeitdetektive messen und schreiben die Zeiten der Kinder auf.

Ablauf und Reflexion:

Zu dieser Turnstunde sind 24 Kinder aus allen Gruppen gekommen. Darunter sind Kinder aller Altersstufen. Von den Zeitdetektiven sind Tim, Mark, Jan, Lukas und Linea dabei. Ich werde von einer Kollegin unterstützt, eine Vorpraktikantin ist auch dabei.

Die Zeitdetektive erfüllen anfangs ihre Aufgaben (Tempo vorgeben durch das Hochhalten der Karten mit den Tiersymbolen, Zeit messen, Tiere erkennen und in die richtigen Häuschen führen). Mit der Zeit möchten sie lieber auch wie die anderen Kinder mitlaufen, Tiere sein. Also übernehme ich einen Teil der Aufgaben.
Die jüngeren Kinder laufen so schnell wie die anderen, sie sind noch nicht in der Lage, sich an die individuellen Vorgaben zu halten. Aus diesem Grund können die Zeitdetektive nur sehr schlecht erkennen, welche Tiere sie sind. Das individuelle Messen jedes Tieres müssen wir durch Gruppenmessen ersetzten (eine zu große Kinderzahl). Die Spielgeschichte: „Wir gehen angeln“ gefällt den Kindern sehr, alle wollen mitmachen. Leider erlaubt es die Zeit nicht. Dazu kommt, dass ich ein größeres Kind als erstes ausgesucht habe, und dieses Kind war so aufgeregt, dass es alle Aufgaben besonders auszelebriert hat, wollte dabei sehr komisch sein. Das nächste Kind war viel schneller. Ich habe den Kindern versprochen, dass wir demnächst dieses Spiel noch mal machen.

Fazit

Die Idee mit den Tieren war gut, die jüngeren Kinder brauchen mehr Wiederholungen, erst dann können die Zeitdetektive ihre Aufgaben richtig erfüllen. Bei einer größeren Kinderzahl sind individuelle Messungen nicht angebracht. Die Zeit von einer Minute ist in der Praxis sehr lang, die schnelleren Kinder durchlaufen die Turnhalle in einer kürzeren Zeit.

Ich habe beschlossen, ein ähnliches Angebot in einer kleinen Gruppe durchzuführen, die Zeitintervalle von einer Minute auf 30 Sekunden zu verkürzen. So werden die Zeitdetektive nicht überfordert und können ihre Aufgaben selbstständig lösen.

Spiele wie „Wir gehen angeln“ können öfters durchgeführt werden.

Sonnenuhr

Am Donnerstag zeigte ich den Kindern ein Buch über die Uhr. Ich habe es auf der Seite geöffnet, wo die Kinder sehen konnten, wie man früher die Zeit gemessen hat.

Ich erzählte, wie die chinesische Feuer-Uhr funktionierte. Dann haben wir gesehen, wie die ägyptische Wasser-Uhr von innen ausgesehen hat.

Wir überlegten, wie man Kerzen zum Zeitmessen benutzt hat.

Dann erkannten die Kinder eine Sand-Uhr. Die ist genauso wie unsere Zahnputz-Uhr.

Danach waren im Buch verschiedene mechanische Uhren gezeigt. Man konnte die Abbildungen aufklappen und schauen, was in der Uhr drin ist. Jan war begeistert von den vielen Zahnrädern. Für jeden Zeiger sind andere Zahnräder da. Für den dicken Stunden-Zeiger dreht sich das Rad langsam, für den Minuten-Zeiger schneller. Am schnellsten dreht sich das Rad für den Sekunden-Zeiger.

Über der Abbildung einer Kiste stand geschrieben: Hier befindet sich die älteste Uhr der Welt. Keiner wusste was gemeint war. Wir öffneten die Klappe: In der Kiste war ein Hahn. „Ja, stimmt“ hat Jan gerufen. „Der Hahn macht jeden Tag Kikeriki“.

Dann entdeckten die Kinder noch eine Uhr.

So was haben sie noch nicht gesehen. Ich sagte, dass es eine Sonnen-Uhr ist, und erklärte, wie sie funktionierte. Ich nahm dazu einen Stock. Die Sonne schien durch das Fenster, und auf dem Tisch konnte man den Schatten des Stockes sehen. Jan weiß, wie die Sonne in verschiedenen Tageszeiten am Himmel steht. Wir überlegten, wo der Schatten beim Sonnenaufgang ist, wo mittags (Jan sagte: der Schatten ist dann sehr kurz) und wo beim Sonnenuntergang. Und plötzlich beschlossen wir, es selber zu versuchen.

Ich holte einen langen Stock, eine Uhr und Kreide. Draußen suchten wir eine geeignete Stelle. Ich steckte den Stock in die Erde. Auf dem Boden warf der Stock einen Schatten. Jan malte einen Strich entlang des Schattens. Von der Uhr hat er die aktuelle Tageszeit abgelesen und neben dem Schatten aufgeschrieben.

 

 

 

Alle paar Minuten wiederholte er diese Tätigkeit. Kurz vor zwölf Uhr begleiteten ihn Max und Mark. Jan erzählte ihnen, was er macht. Auf dem Boden waren schon mehrere Stiche und verschiedene Uhrzeiten. Max half Jan beim Schreiben.

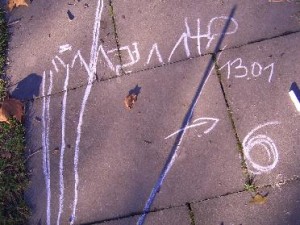Dann habe ich gefragt, ob sie wüssten, wo der Schatten um zwei Uhr sein wird. Max stellte sich auf den zuletzt gemalten Stich und ging entlang weiter, so als ob der Strich sich mit der Zeit verlängern würde. Jan schaute skeptisch und überlegte.

Ich fragte, in welche Richtung bewegt sich der Schatten mit der Zeit? Jan zeigte es sichtig. Ich habe ihn gebeten einen Pfeil zu malen. Dann wiederholte ich die erste Frage. Jan zeigte eine Stelle (die meiner Meinung nach gut geschätzt wurde) und malte einen Kreis drauf.

Kurz vor zwei Uhr waren keine Kinder im Kindergarten. Deshalb habe ich selber einen neuen Strich entlang des Schattens gemalt und die Zeit aufgeschrieben. Nach dem Turnen am Nachmittag sind wir gegen drei Uhr nach draußen gegangen.

Die Kinder sind sofort zu der Sonnen-Uhr gerannt. Auf dem Boden konnte man keinen Schatten mehr sehen. Sie sagten, die Sonne ist nicht mehr da. Tatsächlich war sie hinter einem Haus verschwunden. Wir suchten im Garten nach einer Stelle, von der wir die Sonne noch sehen könnten. Schließlich war sie noch nicht untergegangen. Da war der Rasen heller und der Raureif war geschmolzen.

 

 

 

Im Schatten war der Rasen weiß vom Raureif. In alten Autoreifen entdeckten die Kinder gefrorenes Wasser und beschäftigten sich mit den „Eisbergen“. Die Sonnen-Uhr wurde vergessen, sie ging nicht mehr. Hoffentlich haben wir morgen auch so schönes Wetter wie heute, dann geht die Uhr wieder. Wenn nicht, hoffe ich, dass die Kinder es wissen, wieso sie nicht geht.

 

 

Am nächsten Tag war das Wetter schlecht, der Himmel war bewölkt. Tim und Jan sind zu der Uhr gegangen. Sie merkten, dass auf dem Boden kein Schatten war. Sie wussten, dass es am Wetter lag. Später habe ich sie gefragt, ob die Sonnen-Uhr eine gute Erfindung war. Sie meinten schon, aber bei schlechtem Wetter konnte man nicht wissen, wie spät es ist. „Stimmt“ – habe ich gesagt. „Aus diesem Grund haben die Menschen andere Uhren erfunden, die auch bei schlechtem Wetter gehen“.

Wie lange frühstücken wir?

Zwei Wochen lang haben Tim, Mark, Jan, Linea, Anna und Denise beim Frühstücken die Zeit gemessen, die sie für das Aufessen gebraucht haben. Praktisch ist es so abgelaufen:

  • Das Frühstück wurde ausgepackt, der Zettel mit der Tabelle wurde aus dem Eigentumsfach rausgeholt,
  • das Kind schaute sich das Essen an und benannte die einzelnen Teile, z.B. Apfel, Butterbrot, Joghurt,
  • in der Tabelle wurden Kreuze in die entsprechenden Spalten gemacht,
  • der Timer wurde auf 00:00 eingestellt,
  • das Wort: „Start“ wurde ausgesprochen und die Starttaste betätigt,
  • das Kind fing an zu essen,
  • wenn das Kind fertig war, wurde die Taste „Stopp“ gedrückt,
  • die Zeit wurde vom Timer abgelesen und in die Tabelle geschrieben, der Zettel mit der Tabelle wurde zurück ins Fach gelegt.

Nach Möglichkeit haben die Kinder die Zeiten selbstständig aufgeschrieben. Problematisch war es, wenn mehr als zwei von den oben genannten Kindern gleichzeitig frühstückten. Da mussten wir Erwachsene helfen.

Nach zwei Wochen habe ich die Zettel eingesammelt. Für das weitere Arbeiten habe ich „Minuten-Streifen“ und bunte Stifte auf den Tisch gelegt. Eine Minute ist ein Kästchen auf dem Streifen.

Wie lange eine Minute dauert, haben wir schon bei anderen Spielen erforscht, wir haben auch ein „Minuten-Band“, wo alle Minuten, die wir im Kindergarten verbringen, drauf sind. Für jeden Wochentag haben sich die Kinder eine Farbe ausgesucht. In dieser Farbe wurde das Kästchen mit dem Wochentag und Minuten-Kästchen ausgemalt. Von der Frühstück-Tabelle wurde die Minuten-Zahl entnommen und dann die entsprechende Zahl Minuten-Kästchen ausgemalt. So entstanden Streifen, die die Kinder ausgeschnitten haben. Danach wurden die Streifen passen zu den Tagen in die Tabelle geklebt.

Und dann konnten die Kinder auf Entdeckungsreise gehen:

  • Welcher Streifen ist der längste?
  • Welcher Tag war es?
  • Was hatte ich an diesem Tag mit?
  • Wie lange braucht man für einen Apfel oder Joghurt?
  • Brauche ich für das gleiche Essen auch die gleiche Zeit?
  • Wieso habe ich für wenig so viel Zeit gebraucht?
  • Brauche ich immer lange, oder bin ich manchmal ganz fix?

Bei diesem Angebot lernten die Kinder: einen Timer zu bedienen, eine wissenschaftliche Beobachtung zu führen, die Beobachtung zu dokumentieren, Schlüsse aus den Ergebnissen zu ziehen, über verschiedene Faktoren zu reflektieren: die Art des Lebensmittels, die Menge, das eigene Essverhalten.

Ziel dieser Selbstbeobachtung ist auch zu erkennen, wie viel Zeit von der gesamten Kindergarten-Zeit für das Frühstücken verbraucht wird. Dabei hoffe ich, dass mancher eine Antwort auf die Frage „Wieso konnte ich schon wieder nicht in der Bauecke spielen?“ findet.

Der Kindergarten-Zeit-Streifen

In einem Gespräch habe ich den Kindern den „Kindergarten-Zeit-Streifen“ gezeigt. Der Streifen fängt mit 7:30 Uhr an. Danach folgen alle 270 Minuten, die vollen Stunden sind markiert.

Als Erstes haben wir geguckt, wann der Kindergarten anfängt, wann ich und meine Kollegin in die Gruppe kommen, in welchem Bereich das Frühstücken, Spielen, der Stuhlkreis, das Abholen liegen.

Als nächstes habe ich Fotos von verschiedenen Aktivitäten gemacht, und die Ausdrucke haben die Kinder ausgeschnitten und auf bunte Quadrate geklebt. So gehört die rote Farbe dem Gesellschafts-Spiel, die dunkelblaue dem Zähneputzen, gelb ist Frühstücken, schwarz ist Lego-Spielen usw.

Die Quadrate sind auf einem großen Plakat angebracht. Man kann sie abnehmen und auf den Zeit-Streifen montieren. Man kann auch in der entsprechenden Farbe die Minuten-Kästchen ausmalen und gucken, welche Aktivitäten durchgeführt werden.

Man kann aber auch Zeitdetektiv spielen.

Dieses Spiel geht so: Ein Kind wird zum Zeitdetektiv. Der Zeitdetektiv beobachtet den ganzen Tag ein ausgesuchtes Kind. Zum Detektiv-Werkzeugt gehören: eine Uhr, bunte Stifte und Notizpapier. Der Detektiv achtet darauf, wann das Kind in den Kindergarten kommt, wann es anfängt zu spielen, essen, Zähne zu putzen, malen, wann es fertig ist, wann es abgeholt wird. Jedes Mal wird die Zeit von der Uhr abgelesen und notiert, zusätzlich werden bunte Markierungen gemacht, die den Farben der Quadrate auf dem Plakat entsprechen. An einem anderen Tag wird die Detektivarbeit dokumentiert. Für das beobachtete Kind habe ich einen Zeit-Streifen vorbereitet. Der Detektiv muss nun entsprechende Anfangszeiten suchen und die Minuten-Kästchen in der richtigen Farbe ausmalen.

So kann man die Dauer der Aktivitäten errechnen, den Anteil einer Tätigkeit in der gesamten Kindergartenzeit erkennen. Es sind auch Lücken dabei; das sind Zeiten, wo die Kinder nur zuschauen, sich überlegen, was sie als nächstes tun wollen oder einfach nichts tun.

Tim war der Detektiv bei Mark. An diesem Tag feierte Mark seinen Geburtstag. Ich habe mit Tim abgemacht, dass er mir immer Bescheid sagt, wenn Mark eine neue Tätigkeit anfängt, damit ich Fotos machen kann. So konnte Tim am nächsten Tag bei der Fertigung des Zeitstreifens die Fotos aufkleben. Als der Streifen fertig war, suchten wir nach einem Platz, wo wir ihn aufhängen konnten. Wichtig war, dass er auf Augenhöhe der Kinder hing. So haben wir uns für die Bauecke entschieden.

 

 

Am nächsten Tag freute sich Mark über diese Überraschung. Auch die anderen Kinder interessierten sich dafür.

Meine erste Uhr – ein Bausatz für Kinder

In einem Kindergartenbedarf-Katalog entdeckte ich eine Uhr, die Kinder selber bauen können. Das Gehäuse ist durchsichtig, deshalb können die Kinder sehen, wie die Uhr von innen aussieht. Jan interessiert sich sehr für Mechanik. Er weiß, wie manche Maschinen funktionieren. Als wir das Thema „Vom Korn zum Brot“ hatten, erklärte er uns, wie eine Wassermühle funktioniert. Dabei erwähnte er die vielen Zahnräder und erläuterte, wie sie zusammenarbeiten und die Mühlensteine in Bewegung setzen.

Wir besorgten für die Gruppe einen Satz mit verschiedenen Zahnrädern, damit alle Kinder begreifen können, wie die Kraft von einem Rad auf die nächsten Räder übergeht, welche praktische Bedeutung die Zahl der Zähne hat.

Immer wieder gehen Kinder an die Magnet-Tafel, wo sich die Zahnräder befinden. Sie probieren verschiedene Kombinationen aus, bauen längere Reihen usw. sie sehen, wie die Kraft übertragen wird, sie sehen auch, dass sich die kleinen Räder schneller drehen als die großen. Sie entdecken auch, dass man der Reihe den Schwung mit einem großen Rad leichter geben kann, als mit einem kleineren. Durch das Hantieren entdeckten die Kinder die Gesetzte der Mechanik. Es fehlte nur eine praktische Anwendung der Gesetze.

So haben wir uns entschieden, die Uhr zu bestellen.

An einem Nachmittag wollten wir die Uhr zusammenbauen. Jan ist sehr aufgeregt gewesen, er hielt die Packung fest in der Hand und wollte sofort anfangen. Zuerst mussten wir die Verpackung entfernen. Dann holten wir aus der Schachtel alle Bauteile und die Anleitung.

Jan guckte sich die vielen Zahnräder an, dabei bemerkte er, dass sie Prägungen haben. Ganz schnell begriff er, wie die Räder in die Fassung eingesetzt werden müssen. Sehr schnell war die Uhr fertig gebaut. Leider konnten wir die letzte Klemme nicht befestigen, weil die Öffnung im Gehäuse zu eng war.

Trotzdem versuchten wir die Uhr zum Gehen zu bringen. Das Pendel wollte aber nicht pendeln, wir konnten es nur mit der Hand in Bewegung setzen, und dann bleib es gleich stehen. Ich schaute in die Bauanleitung. Dort stand, dass wir uns nicht entmutigen lassen sollten, sonder prüfen, ob alles richtig sitzt. So haben wir die Uhr aufgemacht und auseinander gebaut. Dann wurden noch mal Schritt für Schritt alle Teile reingesetzt. Jan arbeitete alleine, die anderen Kinder schauten nur zu. Bald war die Uhr fertig, und wir versuchten es noch mal. Leider ohne Erfolg. Wir konnten das Pendel nur mit der Hand durch Anschubsen bewegen, dabei konnten wir sehen, wie die Zahnräder sich drehen. Aber die Uhr ging nicht. Wir ließen uns schon wieder nicht entmutigen und überlegten, wieso es nicht klappte. Vielleicht liegt es an der Klemme, die nicht rein gesteckt werden kann. Ich habe vorgeschlagen, dass ich die Uhr mit nach Hause nehme und meinen Mann frage, ob er die Öffnung erweitern kann. Im Kindergarten haben wir kein Werkzeug für Kunststoff. Jan war einverstanden und half mir beim Verpacken der Uhr.

Leider haben alle Bemühungen nichts gebracht, die Uhr ließ sich nicht zum Gehen bringen.

Ich zeigte sie einem Bekannten, der ein Uhren-Sammler ist und jede Uhr reparieren kann. Er meinte, unsere Uhr wären nicht ordentlich produziert worden, die Teile sind nicht sauber gegossen.

Es ist wirklich schade, dass das Spielzeug für Kinder immer wieder mit wenig Sorgfalt hergestellt wird. Die Enttäuschung war sehr groß.

 

 

Anmerkung Hanna Vock:

Im Jahr 2011 kaufte ich im Museumsshop des Deutschen Museums in Bonn eine baugleiche Uhr. Sie heißt „My First Clock“ und ist auch über amazon erhätlich. Als der Bausatz (33 Teile) fertig zusammen gebaut war, tickte die Uhr zwar sehr laut, lief aber einwandfrei. Da hatten die Projekt-Kinder wirklich Pech gehabt.

„Zähneputzen – Memory-Spiel“

Bei uns im Kindergarten putzen die Kinder ihre Zähne nach dem Frühstück. Sie machen es selbstständig im Waschraum, wo sie ihre Becher und Bürsten an den Handtuchhaken haben. In unserer Gruppe ist es die Regel, dass nur zwei Kinder gleichzeitig Zähne putzen können. Damit die Kinder nicht ständig nachschauen müssen, ob ein Platz frei ist, haben wir „Zahn-Mäuse“ an einer Tafel. Wenn die Mäuse im Nest sind, ist ein Platz frei, wenn beide am Käse sitzen, muss man warten. Einmal im Jahr besucht uns eine Mitarbeiterin des Gesundheitsamtes und erklärt den Kindern, wie die Zähne richtig geputzt werden. In der übrigen Zeit läuft das Zähneputzen weiter und liegt überwiegend in der Verantwortung der Kinder. Die Erzieherinnen unterstützen es nach Möglichkeit, achten darauf, dass die Zahnbürsten rechtzeitig ausgetauscht werden, kontrollieren, ob die Becher sauber gehalten werden, kümmern sich um den Zahncreme-Nachschub.

Und so passiert es immer wieder, dass etwas im Waschraum falsch läuft. Entweder werden die Zahnbürsten vertauscht, oder die Spiegel mit der Zahncreme beschmiert. Manchmal gibt es eine kleine Überschwemmung, weil die Kinder gar nicht die Zähne, sondern die Waschbecken putzen. Manche Kinder verbleiben im Waschraum besonders lange, manche kommen nach 10 Sekunden zurück. Und die Becher sind weiß von den Zahncremeresten usw. Wenn wir es im Stuhlkreis ansprechen, meinen Alle, dass sie richtig ihre Zähne putzen. Unsere Beobachtungen zeigen uns aber, dass das nicht stimmt.

Eines Tages habe ich mit ein paar Kindern über das Zähneputzen gesprochen und wollte herausfinden, ob sie wissen, was man alles machen muss, um die Zähne sauber zu bekommen. Ich stellte die Frage: „Was macht man zuerst?“ Antworten der Kinder: „Zahncreme drauf!“ „Nein, erst das Wasser holen!“ „Nein, erst die Maus!“ Die Kinder geben mir verschiedene Antworten. Demnach würde das „Zähneputzen“ aus Wasser holen, Creme drauf, ausspülen, Maus zurück bestehen. Ich stellte wieder die Frage: „Was macht man zuerst?“

Langsam überlegten wir uns die einzelnen Schritte: die Maus auf den Käse setzen, den Becher holen, Zahncreme aufmachen, eine kleine Menge (Erbsengröße) auf die Bürste herausdrücken, die Tube verschließen, Wasser in den Becher füllen, Zähne bürsten: hin und her, oben und unten ausfegen, ausspucken, ausspülen, die Zahnbürste sauber spülen, auch den Becher, den Mund waschen, den Becher und die Bürste zurück dan den Haken bringen, abtrocknen, in den Gruppenraum gehen und die Maus abmachen.

Wie man bei genauer Überlegung merkt, sind es viele (!) Einzelschritte. Kein Wunder, dass sich nicht jeder alles merken kann. Auch die richtige Reihenfolge ist wichtig. Ich habe vorgeschlagen, eine Foto-Reihe zu machen, um die Kinder beim Zähneputzen zu unterstützen.

Julius und Max wollten mitmachen. Also wurden sie meine Models und achteten darauf, dass ich alles fotografiere. Dabei gaben sie sich besonders viel Mühe.

Am Abend zu Hause habe ich die Bilder ausgedruckt und am nächsten Tag machten wir daraus ein Memory-Spiel.

Es sind 12 Paare, die man finden muss. Die Kinder müssen sehr genau hinschauen, wenn sie die Tätigkeit richtig erkennen wollen. Nach dem Spiel kann man die Karten in der richtigen Reihenfolge legen. Eine schwierigere Variante dieses Spiel ist, die Pärchen von Anfang an in der richtigen Reihenfolge zu suchen. Mit den jüngeren Kindern kann man noch anders spielen. Die erste Hälfte der Karten wird gemeinsam in der richtigen Reihenfolge gelegt. Die anderen Karten werden vermischt und verteilt. Dann verdecken die Kinder reihum die Karten der Reihe, man kann nur die nächste legen. Hat das Kind die Karte nicht, ist das nächste Kind dran. Bei allen möglichen Spielvarianten ist es wichtig, die abgebildete Tätigkeit zu benennen oder an die vorherige anzuschließen, zum Beispiel: „Nach dem Ausspucken den Becher sauber machen“. Durch das Wiederholen des Spiels kann sich der ganze Ablauf des Zähneputzens gedanklich bei den Kinder festigen Bei den sprachbegabten Kindern könnte dieses Spiel eine Möglichkeit sein, Geschichten zu erzählen, wobei die Karten nicht in der Reihenfolge auf dem Tisch liegen. Dann würde die Spielvariante „Chaos im Waschraum“ heißen. Ziel des Spiels ist natürlich, alles in Ordnung zu bringen. (Diese Variante habe ich noch nicht ausprobiert!)

Die gleichen Fotos werden dazu benutzt, ein Plakat herzustellen, das wir im Waschraum aufhängen.

Die „Zahnputzreihe“ kann uns natürlich dazu inspirieren, andere Reihen zu überlegen, zum Beispiel: „Was mache ich, wenn ich mich zum Turnen umziehe?“ oder „Was mache ich, wenn ich eine Sandburg bauen möchte?“ usw.

Ziel dieser Spiele ist es, sich bewusst zu machen, was man gerade tut, was vorher war, was folgt. Was muss ich tun, um mein Ziel zu erreichen, oder was erreiche ich, wenn ich die folgenden Schritte durchführe.

Spiel: „Kennst du die Uhr?“

Inhalt: 4 Tafeln mit Uhren, die bewegliche Zeiger haben, darunter ist eine, die römische Zahlen hat; mehrere kleine Karten, die beidseitig bedruckt sind: auf einer Seite ist die Uhr mit einer bestimmten Zeit, auf der anderen ist diese Zeit als Zahl aufgeschrieben – einmal vormittags, einmal nachmittags. Dieses Spiel kann auf mehrere Arten durchgeführt werden.

Die einfachste Variante wäre, die Zeit von der kleinen Uhr auf die große zu übertragen (Nachahmung). Die älteren Kinder können von der Rückseite die entsprechende Zahl ablesen. Weiter kann die Schwierigkeit gesteigert werden, wenn die Kinder versuchen, die große Uhr entsprechend der Zahl auf der Karte zu stellen. Dann können die Kinder eine beliebige Zeit stellen.

Die rechnerisch begabten Kinder können noch eine Variante spielen:

„Lisa setzte sich um 9:05 an den Frühstückstisch, nach 20 Minuten war sie fertig. Wie spät war es dann?“ oder „Sie wurde um 9:25 fertig, wie lange hat sie gefrühstückt?“

Nebenbei können die Kinder die römischen Zahlen lernen. Das machen sie selbstständig, durch Vergleichen mit den arabischen.

Gespräche über die Zeit

In dieser Zeit führte ich mit den Kindern viele Gespräche über dieses weite Thema. Zum Beispiel:

  • Was ist die Zeit?
  • Wie merkt man die Zeit?
  • War die Zeit schon immer?
  • Kann die Zeit ein Ende haben?
  • Wie verändere ich mich mit der Zeit?
  • Gibt es besondere Zeiten?
  • Wie kann man die Zeit messen?
  • Was ist Adventszeit?
  • Welche Jahreszeiten gibt es?
  • Was würde passieren, wenn die Zeit stehen bleiben würde?

Was ich dabei erfahren habe ist die Tatsache, dass die Kinder die Zeit und die Uhr für das gleiche halten.

Dass die Zeit läuft, erkennt man am Ticken oder am Bewegen der Zeiger. Sieht man gerade die Uhr nicht, gibt es keine Zeit, meinen manche Kinder; andere Kinder würden die Uhr suchen, oder auch horchen – vielleicht hört man sie doch. Diese Kinder spüren es schon, dass die Zeit ständig läuft, aber sie brauchen noch den konkreten Gegenstand.

Erst die älteren oder eben auch jüngere hoch begabte Kinder wissen, dass die Zeit immer läuft, auch wenn man keine Uhr hat. Man erkennt es an der Sonne, an den Veränderungen, daran, dass aus einem Kind ein Erwachsener wird, dann ein Opa und dann stirbt man. Aber die Zeit läuft weiter.

Jan weiß, dass die Zeit mit dem Urknall angefangen hat. Wenn die Erde mit einem Meteoriten kollidiert und kaputt ist, läuft die Zeit weiter, dies kann man von einem anderen Planeten messen.

Jan, Tim und Mark haben zu Hause Bücher über die Uhr (sie sehen die Uhr als ein Messgerät), sie begreifen schon die Natur der Zeit.

Bei Mark hilft die Uhr, seine Angst vor dem alleine gelassen werden zu überwinden, die Zeiger nähern sich ständig und ununterbrochen der Anzeige, wann die Mutter kommt. Wenn die Zeiger 20 vor 12 zeigen und die Kinder in die Garderobe gehen, um sich anzuziehen, dann weiß man ohne zu fragen, dass alle nach draußen gehen.

Auch der Kalender ist den Kindern als ein Zeitmesser bekannt, es gibt Monate, Wochen und Tage. Ein besonderer Monat ist der Dezember. Am ersten Dezember macht man das erste Türchen auf, bis zum Heiligen Abend sind es 24 Türchen. Diese Zeit heißt Advent. Im Advent zündet man die Kerzen am Kranz an, aber es gibt nur 4 Kerzen. Die Kerzen messen die Wochen, die Türchen die Tage. In diesem Jahr war der erste Advent schon im November, aber man durfte noch kein Türchen aufmachen. Es ist so, weil in der Vorweihnachtszeit gleichzeitige zwei Bräuche: Adventskranz und Adventskalender existieren. Tim erkannte, dass der Adventskranz länger als der Adventskalender da ist.

Bei zahlreichen Gesprächen, die in dieser Zeit stattgefunden haben, achteten wir besonders darauf, den Kindern verschiedene Zeitangaben zu verdeutlichen. Was ist ein Wochenende? Wie heißen die Wochenendtage? Was macht man bei uns im Kindergarten an bestimmten Wochentagen? Montags kann man bis 17 Uhr bleiben, dienstags haben die Vorschulkinder ihren Nachmittag, donnerstags turnen wir in der großen Turnhalle und der Freitag ist der „Abbautag“.

Tim, Jan und Mark konnten ihr Wissen und Verstehen beweisen. Im Stuhlkreis warteten sie nicht, bis sie an der Reihe waren, sie wollten die Fragen sofort beantworten. Linea hat sich „korrekt“ gemeldet, wenn sie die Antwort wusste. Anna hat nur zugehört, sie meldete sich nicht. Lukas war meistens mit anderen Sachen beschäftigt. Wenn er warten muss, bis er an die Reihe kommt, „verlässt“ er den Raum oder streitet mit den Nachbarn. Ich kann mir auch vorstellen, dass er wegen seiner Sprachprobleme das Sprechen vor der ganzen Gruppe meidet.

Noch ein Kind zeigte ein besonderes Interesse am Adventskalender. Eigentlich an Zahlen. Er konnte die zweistelligen zahlen benennen, aussuchen, sagen, wie sie geschrieben werden. Er wusste auch die Zahlen für die Wochenendtage. Auch bei anderen Aktivitäten liegt sein Interesse am Zählen, Systematisieren, Ordnen. Der Junge, Sven, ist 3 Jahre und 11 Monate alt. Er kennt sich sehr gut mit verschiedenen Fahrzeugen aus, weiß was ein Gelenkkipper ist – sein Lieblingsbuch heißt: „Fahrzeuge“. Er interessiert sich auch für Buchstaben.

Resümee

Das Thema Zeit ist natürlich noch nicht ausgeschöpft worden. Die Jahreswende bietet die nächste Gelegenheit, sich damit zu beschäftigen. Die Zeitdetektive werden auch in der Zukunft aktiv, es gibt noch so viel zu erforschen.

Bei den anderen Kindern macht sich Verständnis für diese Thematik bemerkbar. Hier haben Max, Jan, Mark, Linea und auch Sven bei der Vermittlung mitgewirkt. So konnte die Gruppe von ihrem Wissen profitieren. Ein Junge fragte, ob er auch den Zettel zum Zeitmessen beim Frühstücken haben darf. So lernte er die Stoppuhr zu bedienen, er schrieb die Minutenzahlen in die Spalten.

Mein Ziel ist es, die hoch begabten und besonders begabten Kinder wahrzunehmen, zu unterstützen und ihre besondere Art in die Gruppe zu integrieren. Sie haben in der Gruppengemeinschaft die gleiche Position wie alle Kinder, erfüllen aber andere, ihnen angepasste Aufgaben. So hoffe ich, profitieren alle davon.

Datum der Veröffentlichung: 5.5.07
Copyright © Klaudia Kruszynski 2006, siehe Impressum .