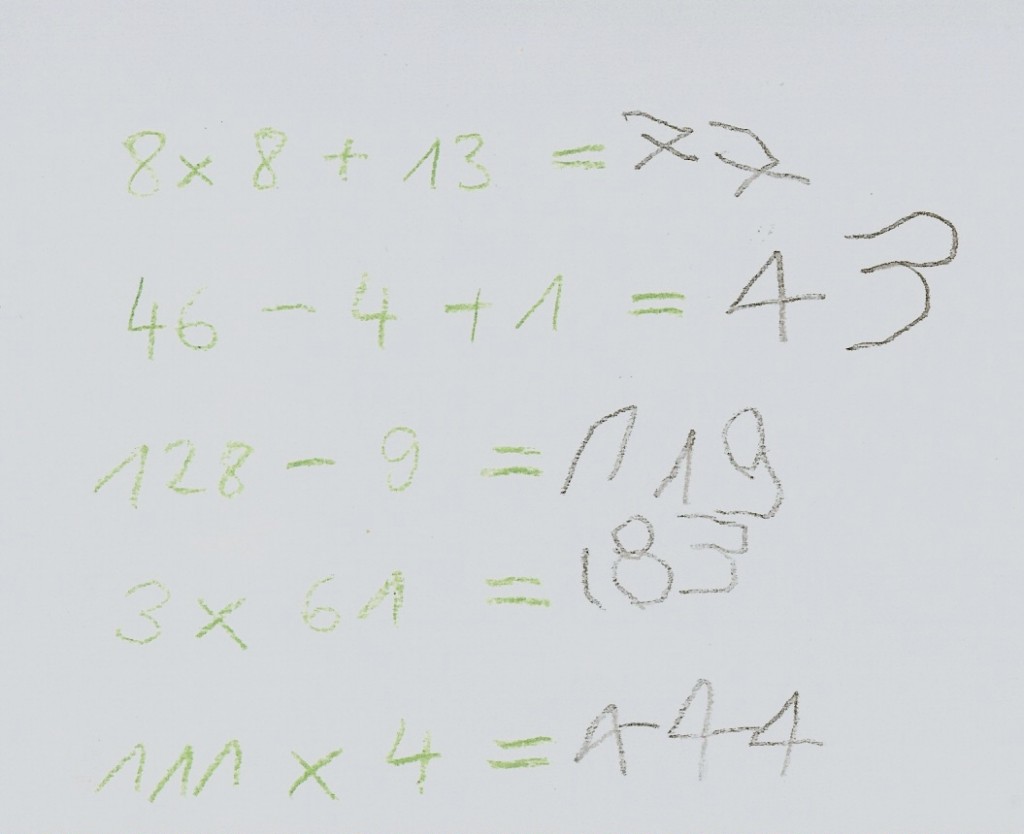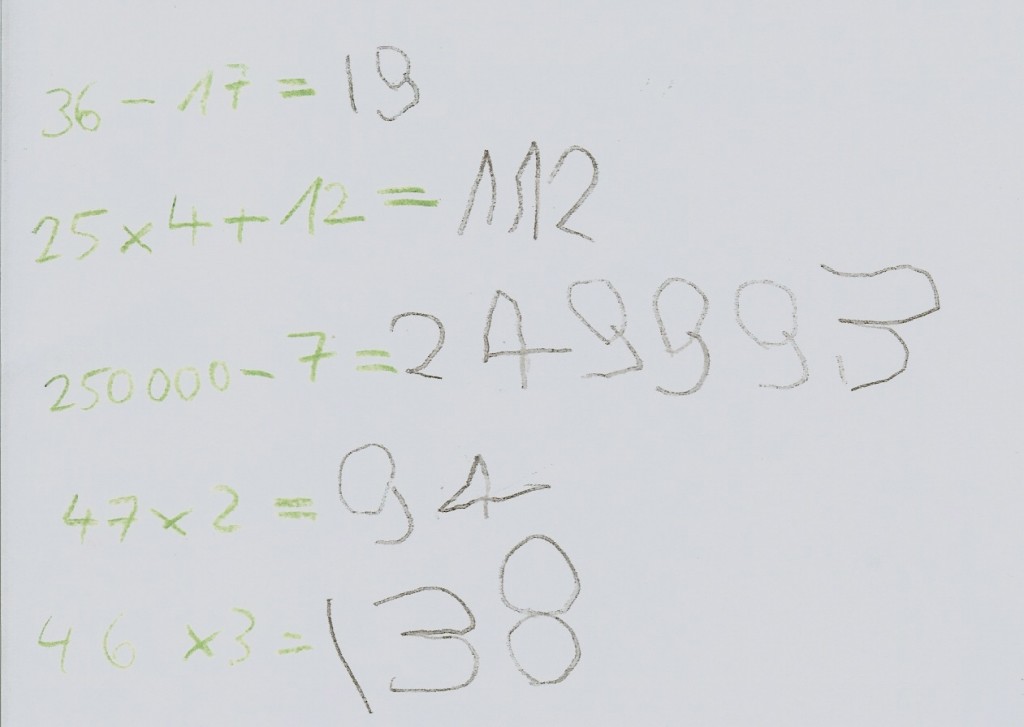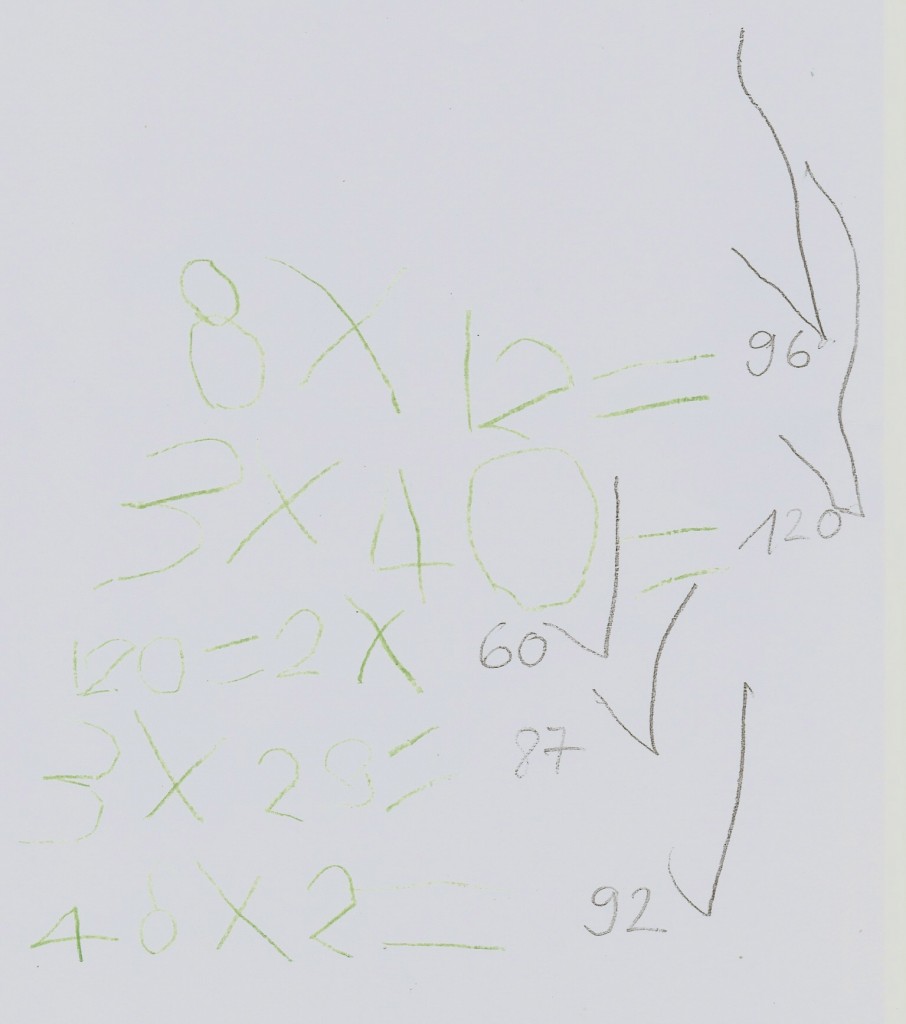All children’s names have been changed.
Back to: Indicators of Possible Intellectual Giftedness
Example by Hanna Vock
At the breakfast table in kindergarten, I am talking to Cathy (6;0) about arithmetic.
As a joke I tell her that instead of 3 x 3 you can also say 3², that „to the power of 2“ means that you should multiply the number by yourself. When I ask her how much 3² is, she answers correctly and after thinking for a moment she can also say how much 4² and 2² are.
Pete (3;5) has no problem grasping the game „Hol´s der Geier“ (see: Interesting Games) right away. He sees immediately, for example, that -3 is more than -5 or that 12 is less than 15. So he knows in every round – without noticeably thinking – who has won the card lying in the middle.
He also understands immediately that he can only win if he has to take as few vulture cards as possible and therefore always places the highest possible number card with the vulture cards. This shows an early developed sense of numbers.
Date of publication in German: August 2021
Example from Edith Baur
I discover Lara´s (4;3 years old) great interest in letters and numbers when I sit with her at the painting table. She points to a sheet of smiley face paper and says, „I have 14 grinning men here.“ I’m amazed. „You can count that far?“ Without hesitation she answers: „Yes – and I can count even further“ and counts to 27 – completely correctly. After that she counts to 100…
She gets up, grabs herself a new empty painting sheet and sits down next to me again.
„I’ll show you what else I can do,“ and she draws all the numbers she can write. „You must see what I’m doing“, she pokes her finger at me when I get distracted for a moment. I apologize and explain to her that I had to answer another kid’s question She’s like, „It’s okay, but you have to look now or you’ll miss out.“
While she now writes more numbers and and also her name, she asks me again and again to look „exactly“ (so she says) to her. Thereby she moves closer and closer to me.
After a few minutes she asks me: „What big numbers can you write?“ As an example, I write a 44 and she asks, „What is the name of this number?“ – „It’s a forty-four.“ She beams at me with her eyes wide open and says: „Look, I can write a 1 and a 2. Is that a twelve then?“ I accept most happily. She gets a red pencil and says: „I’m writing down more, a lot more. Then you can see I’ve been diligent.“
Date of publication: April 2020
Another example from Edith Baur
I also encourage Lara’s great interest in numbers. The game „Sagaland“ gives her the opportunity to do this. She has mastered the rules of the game, which is recommended for children 8 years and older. (Lara is now 4;8.) Among other things, it is important to count dice points and playing fields accurately and to remember them.
Later – Lara is now 4;10 years old – I show her the Montessori hundreds board. I explain to her that she can, among other things, put the number cards up to 100 in the correct order in the frame provided. As there are only a few children left in the group that afternoon, she can once again enjoy tackling this task with me. „It’s really nice when you do the game with me,“ she thanks me.
By 30, she puts the tablets in the frame completely correctly. Then I’m supposed to help her: „Look, Lara, now the number in front doesn’t change yet, but the one behind it. After the zero, you just start again with the one – it will then be 31. After that comes?“ – „The 32,“ she answers with a smile and then places the numbers up to 39. I explain to her that now the front number also changes: „So after the three comes?“
Lara: „The four! And the back number is zero, so 40!“
Date of publication in German: April 2015
Beispiel von Hanna Vock, Bonn
At a parent counselling session one mother showed me pieces of paper. Earlier that morning her son (4;6) had incidentally and quickly written down some math problems on them. He likes it when his parents give him arithmetic problems. He solves them mentally.
And he likes giving his parents problems to solve:
The boy is apparently familiar with three of the four basic mathematical operations and also manages to handle big numbers, too.
Published in German: May 2012
Example by Alexa Kreitlow, Kürten
Ben (4;3) and I are sitting at a table, he is drawing an Easter picture. For a while we are chatting about the things he is drawing.
Suddenly, out of the blue:
“Hey, Alexa, 17 and 3 are odd numbers.”
Me: “What are odd numbers?”
Ben:
“If you’ve got 10 and you take half of it, you got 5. But with 17 and 3 you can’t do that.”
Now I’m all ears, I say: “Boy, you can do real arithmetic. Do you also know what one half of one hundred is?”
Ben looks at me with a serious expression, thinks and says:
His father adds:
“He could have just as well said: > Because I torture mum and dad on every car ride with number-talk and they are so kind as to keep answering.< Seriously though, he likes to do maths and it occupies him a lot.”
Published in German: April 2012
Example by Klaudia Kruszynski, Selm
I ask Tim (4;7) what ever happened to the water pipe he had built. Tim:
“That’s not a water pipe any more, it’s a rocket launcherator. And right there is the water, hot and cold – when the fire is coming out the rocket!”
Next to Tim a pre-school child is playing, it is constructing a rocket. Tim decides he is going to make one, too. He makes a long pole with a sharp point. Then he counts the building blocks he has used up and declares it is now an antenna. Then he makes a small rocket and “flies” it around the table.
The older boy makes a table for the countdown before launch. I tell him, it is called “countdown” and it’s being counted backwards until lift-off: 9,8,7,6,5,4,3,2,1,0!
Suddenly I hear Tim go:
“18,17,16, … .”
“What are you doing?”, I ask him.
“I’m counting down to the start “, he answers and continues his countdown: “… 15,14,13, …”.
In doing so, he pauses shortly sometimes and silently counts forwards, then flips back into backwards. Following the number 12 he does not need any pauses any more. On “0” his rocket lifts off.
I ask: “How fast can rockets fly?”
Tim: “Very fast, because they’re small.”
I ask: “Why does a small rocket fly faster than a big one?”
Tim: “Because it’s got more fire.”
Me: “?”
Tim:
“Because it’s lighter, it weighs only 50 Kilos, a “five” and a “zero”.
Published in German: April 2012
Example from a family (anonymous)
Pete (4;3) asks during dinner:
“Is 8 an even number?”
Counter question: “What is an even number?”
Pete:
“That’s a number you can divide by 2 and there is nothing left. For example, if I have 6 cookies I get 3 and my brother gets 3 and then there’s nothing left. That’s why 6 is an even number. … If I have 7, I’ll have to break one up, but not if it’s 8, then everybody gets 4.“
„Look at that! You know it after all.”
In the same way Pete goes on to examine the numbers 9, 10 , 11 and 12.
At age 5;11 Pete is not only able to read and understand the text of the following problem all by himself, but he even manages to figure out the correct answer.

(A rabbit has 15 children. Each child has 2 balls and 3 dolls and 4 toy cars. How many toys do the children have all together?)
Published in German: April 2012
Example from a family (anonymous)
Benjamin was 3;9 years old when he got interested in the clock face. Since the family had only one conventional clock, the one in the kitchen, and other than that all clocks were digital, Benjamin tried to apply the 24-hour scale to the usual round clock face, as he had seen it in a book.
He very soon understood, that analogue clocks only show 12 hours and the short hand goes round twice every day.

Published in German: December 2011
Example from a family (anonymous)
Janek (2;10):
„Grandma, these are two books and those are two books, too, that makes 4 altogether, so I can have one and you and grandpa and my baby brother can have one, too, but mum can’t have one, too bad …, Mum, I’ll go and get one for you in a minute.”
“But your baby brother doesn’t really need a book, does he?”
He gives it a quick thought and says:
“Then I’ll take his book and mum gets my book.”
“How many do we need then?”
“Four. Just right.”
“Which song should we sing?”
Janek:
“The Lantern Song.”
“Look, there is a table of contents (in the song book). It says on what page we can find it.” He immediately gets the idea and goes:
“That’s 2-7, let me see where that is, … this is where the one is first, but there are the numbers with the two up front … and then the 7 behind it. Right here!”
And he rejoices.
Published in German: April 2011
Example by Hanna Vock, Bonn
Ergün (2;9) is interested in numbers and can read the numerals from 0 to 9. He sees a tram at a station and explains to me:
“That’s the 18, it goes to my house.”
(There are other lines, too, that halt at this station.)
Published in German: April 2011
Example by Birgit Walk, Mechernich
Jonathan (4;9) is being chosen by today’s birthday child to help baking muffins.
Jonathan can read the numbers up to 100 reliably, so he reads out the ingredients listed in the recipe and marks each amount (given in grams) on the scale with an erasable felt pen (the numbers on the scale are in steps of one hundred with subdivisions of 20 grams inscribed with smaller marks.)
He supervises the precise weighing minutely.
Later he sets the correct temperature on the oven.
As the dough is being filled into the muffin pans I overhear him explain to Luis (5 years old): “Look how many rows we can fill with three muffins.” Luis thinks about it and then counts four rows. “So”, concludes Jonathan, “we have 3+3+3+3.” He has ‘marked’ each row with a cue of his finger. He answers my question, as to how many muffins we can bake at the same time: “Twelve”, and Luis gets the same answer by counting. Both children are proud of their result.
Jonathan‘s joy and motivation in dealing with amounts, with the written figures denoting the numbers and the weighing procedure is written in his face.
Example Pete (anonymous)
Pete at the age of 1;3 is playing with a little wooden pot with a lid and he has 3 little stones and 3 little semi-precious stones.
He keeps putting the 6 items inside and then takes them out again. The semi-precious stones are shaped like eggs, they keep rolling away, sometimes he keeps hold of them by sitting on them. Yet he never stops before he has all 6 of them back in the pot, he always gathers all of them. No earlier than that does he begin to take them out again.
Date of publication in German: June 17th, 2010
Example by Heike Brandt, Remscheid
Towards the end of the morning circle it was time for the count up. Carl (3;10) immediately named three children who were missing that day.
On another day towards the end of the afternoon Carl declares that there are now 18 children in the group. I asked him how he got that number. He said that one child had been picked up for home.
Other than that Carl found the count up in the morning circle boring and declined to participate in it.
In a quiz game, when asked about the number of doors in our kindergarten, he almost gets it right and even remarks that the door to the next room is missing. His answer is at first misunderstood by the game host. Upon enquiry he explains himself: “I’m only 3.”
Date of publication: June 17th, 2010
Example Mara (2;6), anonymous observation in the family
For the past few weeks Mara has been showing a marked interest in numbers. Just reading the numbers from 0 to 9 isn’t enough anymore, now she enquires about the meaning of two numbers side by side as in 10 or 12 and so forth …
When we were sorting chestnuts from one bowl to another yesterday, counting them, she instantaneously understood that the ‘one’-digits are always the same and are simply attached to the ‘ten’-digits.
She easily counts up to 20, and when I counted from 21 to 30 for her, she continued from 31 upwards to 50, she did stumble over the ten-numbers (30,40,50).
The inscriptions on our washing machine always get her interested, she wants to know what the numbers under ‘spin cycle’ mean (there the numbers 400/600/900/1200 can be seen), and then she asks me how to say it when the 4 and the 0 and another 0 are set together. Next thing she makes up numbers herself and asks me how to say them, like when the 1 and the 2 are together, and when the 1 and the 2 and the 3 go as one. Then she still continues and wants to know about the 1 with the 2, the 3 and the 4.
Date of publication in German: June 17th, 2010
Example by Monika Meeus, Bornheim
Enno (3;11) was able to recognize numbers very early on. He counts fluently up to 100. When he makes a mistake, he is able to correct himself. He stops shortly, thinks, and is then rather quickly able to say what comes next.
He can read and write numbers. When I write down a bigger number (51, 76 …) he can say it correctly right away.
He can also perform minor calculations. When I praised him for his great skills he replied: “Nobody taught me, I just knew how to do it.”
… We have a sorter toy at our kindergarten. This one consists of a square wooden board with 10 sticks of different length, glued to it and pointing upwards. Then there are 10 square boards with 1 to 10 holes in the same positions as the sticks. The children can slide the boards, one on top of the other, over the sticks to layer the boards. The one with the ten holes goes first. Then one of the sticks doesn’t stick out any longer because it’s too short, and on like that: next the board with 9 holes, in which the second shortest stick disappears. Enno could, at first glance, tell how many sticks and holes there were left, and how many were gone. Great!
Date of publication in German: September 9th, 2009
Example by Inge Förster, Aachen
Felix (4;8) has a good command of the numbers up to 100 and can read two-digit numbers. In exercises to enhance the understanding of basic mathematical concepts and calculations, which we do with our pre-school children, he needs to be given tasks of a higher degree of difficulty. For example, when dealing with the proportions of amounts and sizes by the use of natural objects, we ask the children to hide 10 acorns evenly among 5 places, but we have Felix hide 20 acorns evenly in 4 places.
In a playing situation five children agree to meet at midnight to go on a long night-hike. As his mother is picking him up that afternoon, Felix tells her about it and she reminds him, that he has arranged to see his grandmother the next morning at 8 o’clock. Felix considers this shortly and goes: If I only join them for one hour, I can sleep 6 hours, that’s enough time. I get up at seven and have breakfast until grandma comes.
Felix‘ interest in numbers is increasing rapidly and he keeps demanding higher levels of difficulty, for example the addition of length or weight measures. Or he ponders the question: How many times would our church fit into the Dome of Aachen? A question which has not yet been answered satisfactorily.
Date of publication in German: September 9th, 2009
Example by Hanna Vock, Bonn
Eva was able to read all numbers from 0 to 100 at the age of 3;6.
She understood the concept of decimal positional notation (1-numbers, 10-numbers, 100-numbers) immediately upon this explanation: “At the very back you have the smallest ones, that’s where 4 really stands for 4. On the place next to it you have the next bigger ones, that’s where a 4 is ‘automatically’ a 40. Yet one more place to the left you have the even bigger ones; that’s where a 4 is really a 400.
So 444 is really ‘four hundred – forty – four’.”
She thought it was funny, that it this spoken ‘in reverse’ (the four before the forty!).
[In German two-digit numbers are actually spoken ‘backwards’, 44 is spoken ‘vier-und vierzig’ which is literally ‘four-and forty’. Translator’s note ]
The given explanation was sufficient for her and she went right ahead, trying all kinds of three-digit numbers.
Even the number 305 made her stop and think only shortly, and then she said: “Well, there isn’t one in the middle, so I don’t have to say anything there.”
Michael Hollenbach gives another example in the sleevenotes of his book (Recommended Reading) :
“Helen Wagner is riding her bike across a cemetery together with her 5 years old son. She hears him saying numbers again and again: 86, 22, 64, 80, 3, 77 – finally she realizes that the little know-it-all is calculating the ages at which the deceased had died.”
Date of publication in German: November 20th, 2008
Back to: Indicators of Possible Intellectual Giftedness
Translated by Arno Zucknick.
Copyright © Hanna Vock 2008, see Imprint.